Русский язык (Определение главной информации текста)
Результаты теста
Вопрос №1
1. В пачке 500 листов бумаги формата А4. За неделю расходуется 3350 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на одну неделю?
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
7
Полученные баллы: 0
Вопрос №2
2. На рисунке 30 жирными точками показано суточное количество осадков, выпавших в Дождевске со 2 по 14 марта 1972 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало 4 мм осадков.
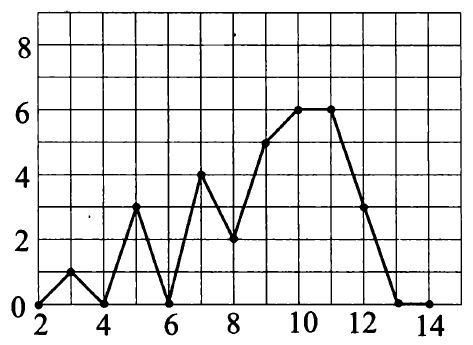
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
7
Полученные баллы: 0
Вопрос №3
3. Автомобильный журнал определяет рейтинги автомобилей на основе показателей безопасности S, комфорта С, функциональности F, качества Q и дизайна D. Каждый отдельный показатель оценивается по 5-балльной шкале. Рейтинг R вычисляется по формуле
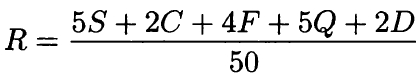
В таблице даны оценки каждого показателя для трёх моделей автомобилей. Определите наивысший рейтинг представленных в таблице моделей автомобилей.
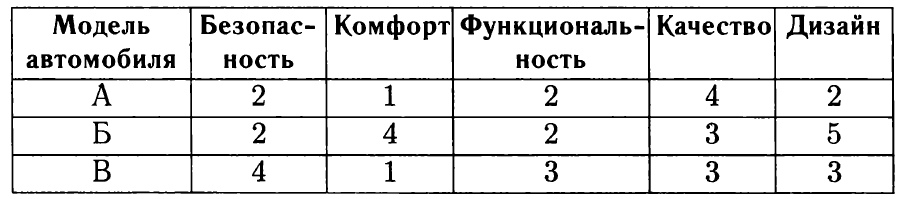
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
1.1
Полученные баллы: 0
Вопрос №4
4. Найдите площадь треугольника, изображённого на рисунке.
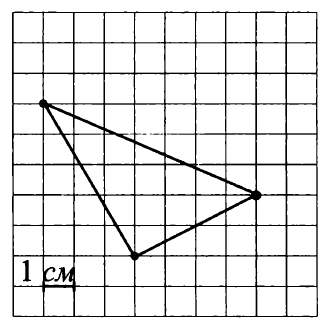
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
13
Полученные баллы: 0
Вопрос №5
5. Вероятность того, что электронная книга прослужит больше трёх лет, равна 0,86. Вероятность того, что она прослужит больше пяти лет, равна 0.72. Найдите вероятность того, что она прослужит меньше пяти лет, но больше трех лет.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
0.14
Полученные баллы: 0
Вопрос №6
6. Найдите корень уравнения ![]()
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
-1
Полученные баллы: 0
Вопрос №7
7. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 12. Найдите площадь этого треугольника.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
36
Полученные баллы: 0
Вопрос №8
8. На рисунке изображён график у = f'(x) — производной функции f(x), определённой на интервале (-3; 3). Найдите точку минимума функции f(x).
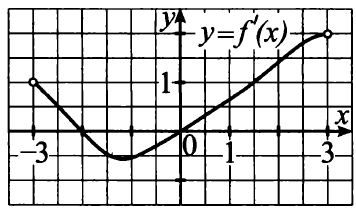
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
0
Полученные баллы: 0
Вопрос №9
9. Во сколько раз увеличится площадь поверхности октаэдра, если все рёбра увеличить в 1,5 раза?
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
2.25
Полученные баллы: 0
Вопрос №10
10. Найдите значение выражения![]()
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
15
Полученные баллы: 0
Вопрос №11
11. На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему ко-ординат: ось Оу направим вертикально вдоль одного из пилонов, а ось Ох направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, имеет уравнение у = 0,008x2 — 0,96x + 45, где х и у измеряются в метрах. Найдите длину ванты, расположенной в 40 метрах от пилона. Ответ дайте в метрах.
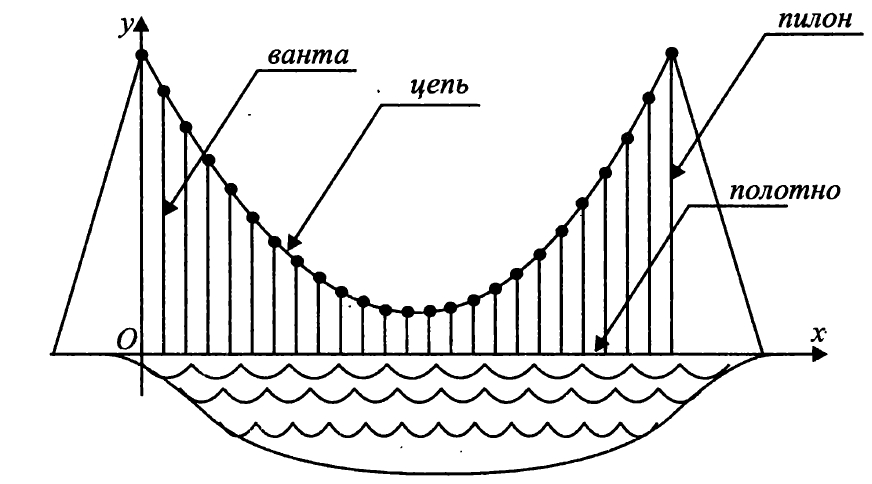
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
19.4
Полученные баллы: 0
Вопрос №12
12. Найдите площадь боковой поверхности многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
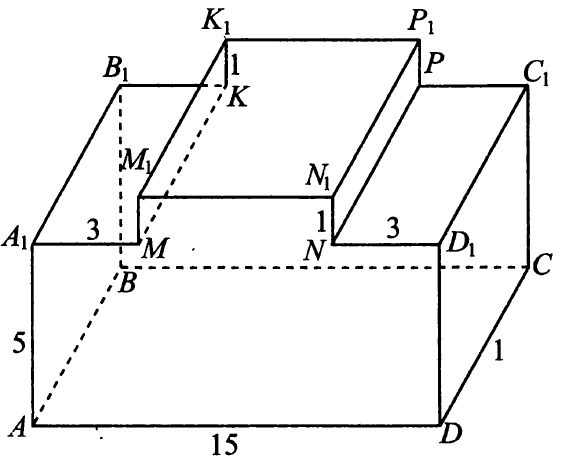
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
210
Полученные баллы: 0
Вопрос №13
13. Заказ на 450 деталей один рабочий выполняет на 15 часов быстрее второго. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 15 деталей больше?
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
15
Полученные баллы: 0
Вопрос №14
14. Найдите точку максимума функции ![]()
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
2
Полученные баллы: 0
Вопрос №15
15.
а) Решите уравнение
![]()
б) Укажите корни этого уравнения, принадлежащие отрезку
(0;3].
Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, ели ответ неверный, то введите знак "-".
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
+
Полученные баллы: 0
Вопрос №16
16. В основание цилиндра высотой 24 и радиусом основания 8 вписан тупоугольный треугольник ABC, в котором ВС = 12, АВ = АС.
а) Постройте сечение призмы ABCA1B1C1 плоскостью, перпендикулярной плоскостям BB1C1C и A1BC и проходящей через точку А, если AA1, BB1 и СC1 — образующие цилиндра.
б) Найдите величину угла между плоскостью В1ВС и А1ВС.
Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, ели ответ неверный, то введите знак "-".
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
+
Полученные баллы: 0
Вопрос №17
17. Решите систему неравенств
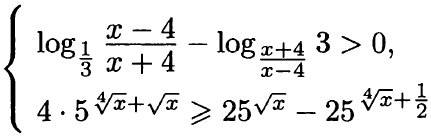
Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-".
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
+
Полученные баллы: 0
Вопрос №18
18. В равнобедренную трапецию вписана окружность.
а) Докажите, что диаметр окружности есть среднее пропорциональное между параллельными сторонами.
б) Найдите радиус этой окружности, если площадь трапеции равна 52, а параллельные стороны относятся как 3 : 5.
Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-".
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
+
Полученные баллы: 0
Вопрос №19
19. Цех сборки может выпускать 50 мотоциклов и 150 скутеров в день. Отдел технического контроля в день может проверить не более 75 изделий. Мотоцикл в полтора раза дороже скутера. Сколько мотоциклов и сколько скутеров нужно выпускать в сутки, чтобы общая стоимость продукции была наибольшей и все изделия были проверены отделом технического контроля?
Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-".
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
+
Полученные баллы: 0
Вопрос №20
20. Найдите все значения параметра а, при которых уравнение
![]()
имеет ровно три корня, расположенных на отрезке
![]()
Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-".
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
+
Полученные баллы: 0
Вопрос №21
21. Бесконечную последовательность b1, b2,b3 ... назовём особенной, если все её члены — натуральные числа, причём для всех n b1 + b2 +... bn-1 < Ьn.
а) Существует ли особенная последовательность, у которой все члены меньше 2015?
б) Существуют ли такая особенная последовательность {bn} и такая геометрическая прогрессия {cn}, что bn - an < 2015 для всех n?
в) Существуют ли такая особенная последовательность {bn} и такая арифметическая прогрессия {an}, что Ьn - an <2015 для всех n?
Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-".
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
+
Полученные баллы: 0


/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_1.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_2.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_3.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_4.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_5.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_6.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_7.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_8.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_9.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_10.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_11.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_12.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_13.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_14.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_15.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_16.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_17.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_18.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_19.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_20.jpg)
/%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82%D0%BE%D0%B2/reshebnik/3/3_21.jpg)