Русский язык (Определение главной информации текста)
Результаты теста
Вопрос 1
Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
7
Полученные баллы: 0
Вопрос 2
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.
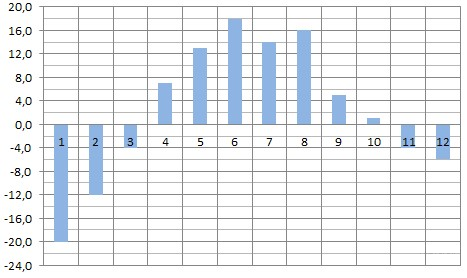
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
16
Полученные баллы: 0
Вопрос 3
Найдите величину угла ABC. Ответ дайте в градусах.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
45
Полученные баллы: 0
Вопрос 4
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
0,52
Полученные баллы: 0
Вопрос 5
Найдите корень уравнения
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
-4
Полученные баллы: 0
Вопрос 6
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
30
Полученные баллы: 0
Вопрос 7
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
0,125
Полученные баллы: 0
Вопрос 8
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
/profil/-11/8.png)
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
4
Полученные баллы: 0
Вопрос 9
Найдите значение выражения
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
-24
Полученные баллы: 0
Вопрос 10
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель − целое число от –2 до 2.
Составители рейтинга считают, что объективность ценится втрое, а информативность публикаций — впятеро дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Если по всем четырем показателям какое-то издание получило одну и ту же оценку, то рейтинг должен совпадать с этой оценкой. Найдите число A, при котором это условие будет выполняться.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
10
Полученные баллы: 0
Вопрос 11
Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
8
Полученные баллы: 0
Вопрос 12
Найдите наибольшее значение функции на отрезке
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
5
Полученные баллы: 0
Вопрос 13
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
Полученные баллы: 0
Вопрос 14
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M.
а) Докажите, что MD : MD1 = 2 : 1.
б) Найдите площадь сечения, если AB = 4, AA1 = 6.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
Полученные баллы: 0
Вопрос 15
Решите неравенство:
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
Полученные баллы: 0
Вопрос 16
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите радиус окружности, описанной около треугольника BCD, если известно, что радиус первой окружности равен 4, а радиус второй окружности равен 1.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
Полученные баллы: 0
Вопрос 17
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
Полученные баллы: 0
Вопрос 18
Найдите все значения параметра a, при каждом из которых система уравнений имеет ровно два решения.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
Полученные баллы: 0
Вопрос 19
На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 2970. В каждом числе поменяли местами первую и вторую цифры (например, число 16 заменили на число 61).
а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 3 раза меньше, чем сумма исходных чисел.
б) Могла ли сумма получившихся чисел быть ровно в 5 раз меньше, чем сумма исходных чисел?
в) Найдите наименьшее возможное значение суммы получившихся чисел.
Ваш ответ:
Вы пропустили вопрос
Правильный ответ:
Полученные баллы: 0

