Русский язык (Определение главной информации текста)
Результаты теста
Затрачено времени:
10:39:17
Вопрос 1
Сколько значащих нулей в двоичной записи десятичного числа 64?
Пояснение
Переведём 64 в двоичную систему счисления и сосчитаем количество нулей:
6410= 10000002
Ваш ответ:
Вы пропустили вопрос
Вопрос 2
Логическая функция F задаётся выражением ¬w ∧ z ∧ (y → x).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|
| ??? |
??? |
??? |
??? |
F |
| 1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
0 |
1 |
1 |
1 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности:
| Переменная 1 | Переменная 1 | Функция |
|---|
| ??? |
??? |
F |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Пояснение
1) Для выполнения таблицы ¬W всегда должно быть равно 1, значит, W равно 0 (2 столбец).
2) Для выполнения таблицы Z всегда должно быть равно 1 (1 столбец).
3) Для выполнения ¬y ∨ x нужно, чтобы не было случая, когда x=0, а y=1, значит, x соответствует третий столбец, а y — 4.
Ваш ответ:
Вы пропустили вопрос
Вопрос 3
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
| |
A |
B |
C |
D |
E |
F |
| A |
|
2 |
4 |
6 |
|
16 |
| B |
2 |
|
|
3 |
|
|
| C |
4 |
|
|
3 |
|
|
| D |
6 |
3 |
3 |
|
4 |
9 |
| E |
|
|
|
4 |
|
3 |
| F |
16 |
|
|
9 |
3 |
|
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
Пояснение
Найдём все варианты маршрутов из A в F и выберем самый короткий.
Из пункта A можно попасть в пункты B, C, D, F.
Из пункта B можно попасть в пункт D.
Из пункта C можно попасть в пункт D.
Из пункта D можно попасть в пункты E, F.
Из пункта E можно попасть в пункт F.
A—B—D—E—F: длина маршрута 12 км.
A—B—D—F: длина маршрута 14 км.
A—C—D—E—F: длина маршрута 17 км.
A—C—D—F: длина маршрута 16 км.
A—D—E—F: длина маршрута 13 км.
A—D—F: длина маршрута 15 км.
A—F: длина маршрута 16 км.
Ваш ответ:
Вы пропустили вопрос
Вопрос 4
Сколько записей удовлетворяют условию «Пол = 'м' и Биология < Обществознание»?
| Фамилия | Пол | Биология | История | Физика | География | Обществознание |
|---|
| Антипенко |
ж |
70 |
72 |
64 |
68 |
77 |
| Багрыненко |
м |
82 |
83 |
56 |
78 |
69 |
| Гатуренко |
ж |
85 |
64 |
81 |
74 |
61 |
| Горыненко |
м |
76 |
68 |
86 |
87 |
67 |
| Жикирко |
м |
61 |
64 |
66 |
78 |
75 |
| Игнатенко |
ж |
72 |
60 |
72 |
70 |
73 |
Пояснение
Условие "Пол = 'м'" верно для "Багрыненко, Горыненко, Жикирко".
Из них "Биология < Обществознание" верно для Антипенко, Жикирко, Игнатенко.
Оба утверждения верны для Жикирко.
Ваш ответ:
Вы пропустили вопрос
Вопрос 5
По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А — 0, Б — 1011. Укажите сумму длин кратчайших кодовых слов для букв В и Г, которые будут удовлетворять условию Фано.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Пояснение
Для двух букв кодовые слова уже известны, осталось подобрать для оставшихся двух букв такие кодовые слова, которые будут являться кратчайшими и удовлетворять условию Фано.
Кодовые слова не могут начинаться с 0, поскольку 0 является кодовым словом для буквы А. Кодовым словом для буквы В будет являться 11. Кодовым словом для буквы Г будет являться 100, кодовое слово 101, поскольку кодовым словом для буквы Б является 1011.
Таким образом, сумма кратчайших кодовых слов для букв В и Г будет равна 2 + 3 = 5.
Ваш ответ:
Вы пропустили вопрос
Вопрос 6
Исполнитель Чертежник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остается след в виде прямой линии. У исполнителя существуют следующие команды:
Сместиться на вектор (а, Ь) – исполнитель перемещается в точку, в которую можно попасть из данной, пройдя а единиц по горизонтали и b – по вертикали.
Запись: Повторить 5[ Команда 1 Команда 2] означает, что последовательность команд в квадратных скобках повторяется 5 раз.
Чертежник находится в начале координат. Чертежнику дан для исполнения следующий алгоритм:
Сместиться на вектор (5,2)
Сместиться на вектор (-3, 3)
Повторить 3[Сместиться на вектор (1,0)]
Сместиться на вектор (3, 1)
На каком расстоянии от начала координат будет находиться исполнитель Чертежник в результате выполнения данного алгоритма?
Пояснение
Конечная точка будет обладать координатами по оси x и y. Эти координаты можно складывать независимо друг от друга.
Найдём значение x: 5 - 3 + 1 + 1 + 1 + 3 = 8.
Найдём значение y: 2 + 3 + 1 = 6.
Расстояние от начала координат находится по формуле:  , поэтому
, поэтому
 .
.
Ваш ответ:
Вы пропустили вопрос
Вопрос 7
Дан фрагмент электронной таблицы:
| |
A |
B |
C |
| 1 |
3 |
5 |
|
| 2 |
=2C1−11 |
=C1+1 |
=B1(C1−A1*3)−2 |

Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:С2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.
Пояснение
Заполним таблицу:
| |
A |
B |
C |
| 1 |
3 |
5 |
|
| 2 |
=2C1−11 |
=C1+1 |
=5(C1−9)−2 |
Из диаграммы заметим, что значения в ячейках равны. Приравняем значения в ячейках A2 и B2: 2C1 − 11 = C1 + 1, откуда C1 = 12. Подставив найденное значение, убеждаемся, что значения во всех ячейках равны.
Ваш ответ:
Вы пропустили вопрос
Вопрос 8
Определите, что будет напечатано в результате выполнения программы (записанной ниже на разных языках программирования):
| Бейсик | Паскаль |
|---|
DIM N, S AS INTEGER
N = 0
S = 512
WHILE S >= 0
S = S - 20
N = N + 1
WEND
PRINT N
|
var n, s: integer;
begin
n := 0;
s := 512;
while s >= 0 do
begin
s := s - 20;
n := n + 1
end;
write(n)
end.
|
| Си++ | Алгоритмический язык |
|---|
#include <iostream>
using namespacestd;
int main()
{
int n, s;
n = 0;
s = 512;
while (s >= 0)
{
s = s - 20;
n = n + 1;
}
cout « n « endl;
}
|
алг
нач
цел n, s
n := 0
s := 512
нцпока s >= 0
s := s - 20
n := n + 1
кц
вывод n
кон
|
| Python |
|---|
n = 0
s = 512
while s >= 0:
s -= 20
n += 1
print(n)
|
Пояснение
Цикл while выполняется до тех пор, пока истинно условие s >= 0, т. е. переменная s определяет, сколько раз выполнится цикл.
Так как  , цикл выполнится 26 раз (так как действие "s := s - 20" выполняется до "n := n + 1", значит, до того, как цикл прервется, действие "n := n + 1" успеет выполниться). Значение n будет равно 26.
, цикл выполнится 26 раз (так как действие "s := s - 20" выполняется до "n := n + 1", значит, до того, как цикл прервется, действие "n := n + 1" успеет выполниться). Значение n будет равно 26.
Ваш ответ:
Вы пропустили вопрос
Вопрос 9
Сколько секунд потребуется модему, передающему сообщения со скоростью 14400 бит/с, чтобы передать цветное растровое изображение размером 640 на 480 пикселей, при условии, что цвет каждого пикселя кодируется 24 битами?
Пояснение
Время t вычисляется по формуле t = Q / q, где Q — объем файла, q — cкорость передачи данных.
Один цвет занимает один пиксел, поэтому Q = 640 * 480 * 24 бит = 7 372 800 бит.
t = 7 372 800 бит / 14 400 бит/с = 512 с.
Ваш ответ:
Вы пропустили вопрос
Вопрос 10
Азбука морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т. д.) можно закодировать, используя код азбуки Морзе длиной не менее трех и не более пяти сигналов (точек и тире)?
Пояснение
Если в алфавите  символов, то количество всех возможных «слов» (сообщений) длиной
символов, то количество всех возможных «слов» (сообщений) длиной  равно
равно  .
.
Нужно определить количество всех трёх-, четырех- и пятибуквенных слов в двоичном алфавите:

Ваш ответ:
Вы пропустили вопрос
Вопрос 11
Алгоритм вычисления значения функции F(n), где n - натуральное число, задан следующими соотношениями:
F(1)= 1;
F(n) = 2*F(n-1) +1 при n >1.
Чему равно значение функции F(6)?
В ответе запишите только натуральное число.
Пояснение
Последовательно находим:
F(1) = 1,
F(2) = 3,
F(3) = 7,
F(4) = 15,
F(5) = 31,
F(6) = 63.
Таким образом, ответ 63.
Ваш ответ:
Вы пропустили вопрос
Вопрос 12
В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.
По заданным IP-адресу узла и маске определите адрес сети.
IP –адрес узла: 224.24.254.134
Маска: 255.255.224.0
При записи ответа выберите из приведенных в таблице чисел четыре элемента IP-адреса и запишите в нужном порядке соответствующие им буквы, без использования точек.
| A |
B |
C |
D |
E |
F |
G |
H |
| 255 |
254 |
244 |
224 |
134 |
24 |
8 |
0 |
Пример.
Пусть искомый IP-адрес 192.168.128.0, и дана таблица
| A |
B |
C |
D |
E |
F |
G |
H |
| 128 |
168 |
255 |
8 |
127 |
0 |
17 |
192 |
В этом случае правильный ответ будет записан в виде: HBAF
Пояснение
1. Запишем числа маски сети в двоичной системе счисления.



2. Адрес сети получается в результате поразрядной конъюнкции чисел маски и чисел адреса узла (в двоичном коде). Так как конъюнкция 0 с чем-либо всегда равна 0, то на тех местах, где числа маски равны 0, в адресе узла стоит 0. Аналогично, там, где числа маски равны 255, стоит само число, так как конъюнкция 1 с любым числом всегда равна этому числу.
3. Рассмотрим конъюнкцию числа 224 с числом 254.


Результатом конъюнкции является число 224.
4. Сопоставим варианты ответа получившимся числам: 224, 24, 224, 0.
Ваш ответ:
Вы пропустили вопрос
Вопрос 13
Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля — ровно 9 символов. В качестве символов могут быть использованы десятичные цифры и 29 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и прописные (регистр буквы имеет значение!). Под хранение каждого такого пароля на компьютере отводится одинаковое и минимально возможное целое количество байтов. При этом используется посимвольное кодирование, и все символы кодируются одинаковым и минимально возможным количеством битов. Определите объём памяти, который используется для хранения 20 паролей. (Ответ дайте в байтах.)
Пояснение
Всего для кодирования может быть использовано 10 десятичных цифр, 29 строчных и 29 прописных букв, т. е. 10 + 29 + 29 = 68 символов. Известно, что с помощью N бит можно закодировать 2N различных символов. Поскольку 26 < 68 < 27 и для каждого пароля число бит одинаково, то для записи каждого из 9 символов необходимо 7 бит памяти. Для хранения всех 9 символов номера нужно 63 бит, а т. к. для записи используется целое число байт, то необходимо округлить в большую сторону число 63 до числа, кратного восьми, это число 64 = 8 · 8 бит (8 байт). Поэтому для хранения 20 паролей понадобится 20 · 8 = 160 байт.
Ваш ответ:
Вы пропустили вопрос
Вопрос 14
Исполнитель Редактор получает на вход строку цифр и преобразует её.
Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно). Часть ИНАЧЕ может отсутствовать, в этом случае, если условие ложно, никакие действия не выполняются.
Какая строка получится в результате применения приведённой ниже программы к строке вида 1…12…2 (7 единиц, затем 7 двоек)? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (111) ИЛИ нашлось (222)
ЕСЛИ нашлось (111)
ТО заменить (111, 2)
КОНЕЦ ЕСЛИ
ЕСЛИ нашлось (222)
ТО заменить (222, 1)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Пояснение
Данный алгоритм сначала заменит 6 первых единиц на 2 двойки. Получим: 221 222 222 2. Далее произойдет замена 6-ти двоек (221 222 222 2) на 2 единицы, будет 221 112. Предпоследним шагом заменим 3 единицы на 1 двойку: 222 2. Последним шагом получим 12.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
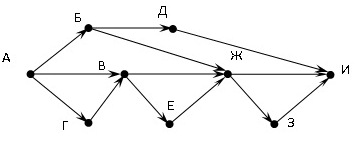
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И?
Пояснение
Начнем считать количество путей с конца маршрута – с города И. NX — количество различных путей из города А в город X, N — общее число путей.
В "И" можно приехать из Д, Ж, или З, поэтому N = NИ = NД + NЖ + N З (1)
Аналогично:
NД = NБ;
NЖ = NБ + NВ + NЕ;
NЗ = NЖ.
Добавим еще вершины:
NБ = NА = 1;
NВ = NА + NГ = 1 + 1 = 2;
NЕ = NВ = 2;
NГ = NА = 1;
Преобразуем первые вершины с учетом значений вторых:
NД = NБ = 1;
NЖ = NБ + NВ + NЕ = 1 + 2 + 2 = 5;
NЗ = NЖ = 5.
Подставим в формулу (1):
N = NК = 1 + 5 + 5 = 11.
Начнем считать количество путей с конца маршрута – с города И. NX — количество различных путей из города А в город X, N — общее число путей.
В "И" можно приехать из Д, Ж, или З, поэтому N = NИ = NД + NЖ + N З (1)
Аналогично:
NД = NБ;
NЖ = NБ + NВ + NЕ;
NЗ = NЖ.
Добавим еще вершины:
NБ = NА = 1;
NВ = NА + NГ = 1 + 1 = 2;
NЕ = NВ = 2;
NГ = NА = 1;
Преобразуем первые вершины с учетом значений вторых:
NД = NБ = 1;
NЖ = NБ + NВ + NЕ = 1 + 2 + 2 = 5;
NЗ = NЖ = 5.
Подставим в формулу (1):
N = NК = 1 + 5 + 5 = 11.
Ваш ответ:
Вы пропустили вопрос
Вопрос 16
Сколько единиц содержится в двоичной записи значения выражения: 4511 + 2511 − 511?
Пояснение
Преобразуем выражение: 4511 + 2511 − 511 = 21022 + 2511 − 29 + 1.
Значит, в двоичной записи есть единица, нам нужно занять из 512 позиции единицу, чтобы вычесть 29, тогда будет единица с 511 по 10 позицию. Всего таких позиций 502. Также присутствует единица на последнем и на 1022 месте. То есть всего их будет 502 + 1 + 1 = 504.
Ответ: 504.
Ваш ответ:
Вы пропустили вопрос
Вопрос 17
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц
(в тысячах) |
|---|
| лук | арбалет |
426 |
| лук | чеснок |
414 |
| арбалет & чеснок |
0 |
| лук | арбалет | чеснок |
480 |
Какое количество страниц (в тысячах) будет найдено по запросу лук?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Пояснение
Представим таблицу в виде кругов Эйлера. Пусть арбалет — круг 1, лук — круг 3, чеснок — круг 5. Тогда задача — найти количество элементов N в областях 2, 3, 4: N2 + N3 + N4. По таблице известно:
N1 + N2 + N3 + N4= 426. (1)
N2 + N3 + N4 + N5 = 414. (2)
N1 + N2 + N3 + N4 + N5 = 480. (3)
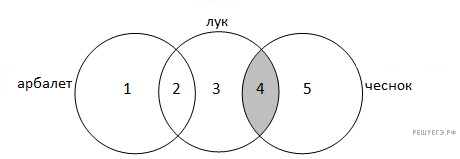
Подставим первое уравнение в третье и найдём N5: N5 = 480 − 426 = 54. После этого подставим второе уравнение в третье и найдём N1: N1 = 480 − 414 = 66. Теперь можем найти количество элементов в областях 2, 3 и 4. Для этого вычтем из третьего уравнения N1 и N5: N2 + N3 + N4 = 480 − 54 − 66 = 360.
Таким образом, N2 + N3 + N4 = 360.
Ваш ответ:
Вы пропустили вопрос
Вопрос 18
На числовой прямой задан отрезок A. Известно, что формула
((x ∈ A) → (x2 ≤ 81)) ∧ ((y2 ≤ 36) → (y ∈ A))
тождественно истинна при любых вещественных x и y. Какую наибольшую длину может иметь отрезок A?
Пояснение
Раскрывая импликацию по правилу A → B = ¬A + B, заменяя логическую сумму совокупностью, а логическое произведение системой соотношений, определим значения параметра А, при котором система совокупностей

будет иметь решения для любых вещественных чисел.
Чтобы решениями системы были все вещественные числа, необходимо и достаточно, чтобы решениями каждой из совокупностей были все вещественные числа.
Решениями неравенства  являются все числа из отрезка [−9; 9]. Чтобы совокупность выполнялась для всех вещественных чисел, числа x, не лежащие на указанном отрезке, должны принадлежать отрезку A. Следовательно, отрезок A не должен выходить за пределы отрезка [−9; 9].
являются все числа из отрезка [−9; 9]. Чтобы совокупность выполнялась для всех вещественных чисел, числа x, не лежащие на указанном отрезке, должны принадлежать отрезку A. Следовательно, отрезок A не должен выходить за пределы отрезка [−9; 9].
Аналогично, решениями неравенства  являются числа из лучей
являются числа из лучей  и
и  Чтобы совокупность выполнялась для всех вещественных чисел, числа x, не лежащие на указанных лучах, должны лежать на отрезке A. Следовательно, отрезок A должен содержать в себе отрезок [−6; 6].
Чтобы совокупность выполнялась для всех вещественных чисел, числа x, не лежащие на указанных лучах, должны лежать на отрезке A. Следовательно, отрезок A должен содержать в себе отрезок [−6; 6].
Тем самым, наибольшая длина отрезка A может быть равна 9 + 9 = 18.
Ваш ответ:
Вы пропустили вопрос
Вопрос 19
Представленный ниже на пяти языках программирования фрагмент программы обрабатывает элементы одномерного целочисленного массива A с индексами от 0 до 9. Перед началом выполнения данного фрагмента эти элементы массива имели значения 3, 5, 8, 2, 1, 4, 3, 1, 2, 6 (т.е. A[0] = 3, A[1] = 5, …, A[9] = 6). Определите значение переменной s после выполнения фрагмента.
| Бейсик | Python |
|---|
s = 0
FOR i = 0 TO 8
IF A(i) < A(9) THEN
t = A(i)
A(i) = A(8 − i)
A(8 − i) = t
s = s + t
END IF
NEXT i
|
s = 0
for i in range(0, 9):
if A[i] < A[9]:
t = A[i]
A[i] = A[8 − i]
A[8 − i] = t
s = s + t
|
| Паскаль | Алгоритмический язык |
|---|
s := 0;
for i:=0 to 8 do begin
if A[i] < A[9] then begin
t := A[i];
A[i] := A[8 − i];
A[8 − i] := t;
s := s + t;
end;
end;
|
s := 0
нц для i от 0 до 8
если A[i] < A[9] то
t := A[i]
A[i] := A[8 − i]
A[8 − i] := t
s := s + t
все
кц
|
| С++ |
|---|
s = 0;
for (i = 0; i <= 8; ++i) {
if (A[i] < A[9]) {
t = A[i];
A[i] = A[8 − i];
A[8 − i] = t;
s = s + t;
}
}
|
Пояснение
Данный алгоритм меняет местами текущий элемент массива и элемент массива, номер которого вычисляется путём вычитания из 8 номера текущего элемента массива, после чего к переменной s прибавляется значение элемента массива, номер которого вычисляется путём вычитания из 8 номера текущего элемента массива, если текущий элемент массива меньше последнего элемента массива.
Изначальный порядок значений: 3, 5, 8, 2, 1, 4, 3, 1, 2, 6.
Первое изменение элементов: 2, 5, 8, 2, 1, 4, 3, 1, 3, 6, s = s + 3.
Второе изменение элементов: 2, 1, 8, 2, 1, 4, 3, 5, 3, 6, s = s + 5.
Третье изменение элементов: 2, 1, 8, 4, 1, 2, 3, 5, 3, 6, s = s + 2.
Четвёртое изменение элементов: 2, 1, 8, 4, 1, 2, 3, 5, 3, 6, s = s + 1.
Пятое изменение элементов: 2, 1, 8, 2, 1, 4, 3, 5, 3, 6, s = s + 2.
Шестое изменение элементов: 2, 1, 3, 2, 1, 4, 8, 5, 3, 6, s = s + 3.
Седьмое изменение элементов: 2, 5, 3, 2, 1, 4, 8, 1, 3, 6, s = s + 5.
Последнее изменение элементов: 3, 5, 3, 2, 1, 4, 8, 1, 2, 6, s = s + 3.
Таким образом, значение переменной s после выполнения фрагмента программы равняется 
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Ниже на пяти языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: a и b. Укажите наибольшее из таких чисел x, при вводе которого алгоритм печатает сначала 2, а потом 4.
| Бейсик | Python |
|---|
DIM X, A, B AS INTEGER
INPUT X
A = 0: B = 0
WHILE X > 0
IF X MOD 2 = 0 THEN
A = A + 1
ELSE
B = B + X MOD 10
END IF
X = X 10
WEND
PRINT A
PRINT B
|
x = int(input())
a=0; b=0
while x > 0:
if x%2 == 0:
a += 1
else:
b += x%10
x = x//10
print(a, b)
|
| Паскаль | Алгоритмический язык |
|---|
var x, a, b: longint;
begin
readln(x);
a := 0; b := 0;
while x > 0 do
begin
if x mod 2= 0 then
a := a + 1
else
b := b + x mod 10;
x := x div 10;
end;
writeln(a); write(b);
end.
|
алг
нач
цел x, a, b
ввод x
a := 0; b := 0
нц пока x > 0
если mod(x,2)=0
то a := a+1
иначе b := b + mod(x,10)
все
x := div(x,10)
кц
вывод a, нс, b
кон
|
| Си++ |
|---|
#include <iostream>
using namespacestd;
int main()
{
int x, a, b;
cin >> x;
a = 0; b = 0;
while (x > 0) {
if (x%2 == 0) a += 1;
else b += x%10;
x = x / 10;
}
cout << a << endl << b << endl;
return 0;
}
|
Пояснение
Данный алгоритм, получая на вход число x, считает количество четных цифр и складывает нечетные.
Эта часть программы считает количество четных цифр:
if x mod 2 = 0 then
a := a + 1
А эта — пока число не станет равным нулю — складывает нечетные цифры, а также убирает последнюю цифру числа:
while x > 0 do
begin
...
else
b := b + x mod 10;
x := x div 10;
Таким образом, необходимо найти наибольшее число x, в котором 2 четных цифры, а сумма нечетных равна 4. Для этого помещаем в начало записи числа две наибольшие натуральные четные цифры, а потом для увеличения количества разрядов минимально возможные нечетные. Получаем 881111.
Ваш ответ:
Вы пропустили вопрос
Вопрос 21
Определите, какое число будет напечатано в результате выполнения следующего алгоритма (для Вашего удобства алгоритм представлен на четырёх языках программирования).
| Бейсик | Паскаль |
|---|
DIM A, B, T, N AS INTEGER
A = -20: B = 20
N = 0
FOR T = A TO B
IF F(T) >= 0 THEN
N = N+1
END IF
NEXT T
PRINT N
FUNCTION F(x)
F = 16*(9-x)*(9-x)+127
END FUNCTION
|
var a, b, t, N :integer;
Function F(x: integer):integer;
begin
F := 16*(9-x)*(9-x)+127;
end;
BEGIN
a := -20; b := 20;
N := 0;
for t := a to b do begin
if (F(t) >= 0) then begin
N := N+1;
end;
end;
write(N);
END.
|
| Си++ | Алгоритмический |
|---|
#include <iostream>
using namespacestd;
int F(int x)
{
return 16*(9-x)*(9-x)+127;
}
int main()
{
int a, b, t, N;
a = -20; b = 20;
N = 0;
for (t=a; t<=b; t++){
if (F(t) >= 0) {
N++;
}
}
cout « N « endl;
}
|
алг
нач
цел a, b, t, N
a := -20; b := 20
N := 0
нц для t от a до b
если F(t) >= 0
то
N := N+1
все
кц
вывод N
кон
алг цел F(цел x)
нач
знач := 16*(9-x)*(9-x)+127
кон
|
| Python |
|---|
def f(x):
return 16*(9-x)*(9-x)+127
a = -20
b = 20
N = 0
for t in range(a, b+1):
if (f(t) >= 0):
N += 1
print(N)
|
Пояснение
Алгоритм предназначен для нахождения количества целых точек на отрезке [−20; 20] в которых функция F(x) = 16 · (9 − x)2+127 имеет значение большее, либо равное нулю. Следовательно, задачу можно свести к неравенству:

Данное неравенство будет выполнятся во всех целых точках отрезка [−20; 20]. Всего отрезок [−20; 20] содержит 41 целую точку. Следовательно, ответ 41.
Ваш ответ:
Вы пропустили вопрос
Вопрос 22
Исполнитель ТренерБ преобразует число, записанное на экране. У исполнителя три команды, которым присвоены номера:
1. Прибавь 1
2. Прибавь 2
3. Прибавь 6
Первая из них увеличивает число на экране на 1, вторая увеличивает это число на 2, а третья — на 6. Программа для исполнителя ТренерБ — это последовательность команд. Сколько существует программ, которые число 21 преобразуют в число 30?
Пояснение
Для сложения справедлив переместительный (коммутативный) закон, значит, порядок команд в программе не имеет значения для результата.
Все команды увеличивают исходное число, поэтому количество команд не может превосходить (30 − 21) = 9. При этом минимальное количество команд — 3.
Порядок команд не имеет значения, каждому числу команд соответствует один набор команд, которые можно расположить в любом порядке.
Рассмотрим все возможные наборы и вычислим количество вариантов рассположения команд в них.
Набор 1 1111 1111 имеет один возможный вариант.
Набор 1111 1112 — 8 вариантов.
Набор 111 1122 — 21 возможный вариант расположения: это число перестановок с повторениями 7!/(5!·2!).
Набор 11 1222 — 20 вариантов.
Набор 1 2222 — 5 вариантов.
Набор 1 113 — 4 варианта.
Набор 123 — 6 вариантов: это число перестановок: 3!.
Всего имеем: 1 + 8 + 21 + 20 + 5 + 4 + 6 = 65 программ.
Ваш ответ:
Вы пропустили вопрос
Вопрос 23
Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1
(y5 → y4) ∧ (y4 → y3) ∧ (y3 → y2) ∧ (y2 → y1 ) = 1
x3 ∧ y3 = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Пояснение
1) Из последнего уравнения следует, что глобально мы имеем x3=1, y3=1.
2) Логическое И истинно, только тогда, когда истины все утверждения, а импликация ложна только в случае, если из истинного следует ложное.
3) Уравнение (1) описывает ряд переменных {x1, x2, x3, x4, x5}. Так как из переменной с более низким номером всегда следует переменная с более высоким, если любую переменную из этого ряда приравнять 1, то все следующие должны также быть равны 1. Для уравнения (2) существует то же самое правило, только наоборот: из переменной с более высоким номером всегда следует переменная с более низким. Иначе говоря, если записать переменные x в порядке возрастания их номеров, справа будут единицы, а слева — нули, в y — напротив, слева единицы, справа - нули.
4) Рассмотрим вариант x3=1, y3=1. Тогда все следующие: x4, x5, y2, y1 тоже равны 1. Остаются переменные x1, x2, y4, y5. Так как x2 следует из x1, для них мы имеем 3 варианта, аналогично для y4 и y5. 3 3=9.
3=9.
Ответ — 9.
Ваш ответ:
Вы пропустили вопрос
Вопрос 24
Дано целое положительное число N, не превосходящее 1000. Необходимо определить, является ли это число степенью числа 3. То есть требуется определить, существует ли такое целое число K, что 3K = N, и вывести это число либо сообщение, что такого числа не существует.
Для решения этой задачи ученик написал программу, но, к сожалению, его программа оказалась неверной. Ниже эта написанная им программа для Вашего удобства приведена на пяти языках программирования.
| Бейсик | Python |
|---|
DIM N, K AS INTEGER
INPUT N
K = 0
WHILE K MOD 3 = 0
K = K + 1
N = N 3
WEND
IF N > 0 THEN
PRINT K
ELSE
PRINT "Не существует"
END IF
END
|
n = int(input())
k = 0
while k%3 == 0:
k = k + 1
n = n // 3
if n > 0:
print(k)
else:
print("Не существует")
|
| Паскаль | Алгоритмический язык |
|---|
var n, k: integer;
begin
read(n);
k := 0;
while k mod 3 = 0 do begin
k := k + 1;
n := n div 3;
end;
if n > 0 then
writeln(k)
else
writeln('Не существует')
end.
|
алг
нач
цел n, k
ввод n
k := 0
нц пока mod(k, 3)=0
k := k + 1
n := div(n,3)
кц
если n > 0
то вывод k
иначе вывод "Не существует"
все
кон
|
| Си++ |
|---|
#include <iostream>
using namespacestd;
int main(){
int n, k;
cin >> n;
k = 0;
while (k%3 == 0) {
k = k + 1;
n = n / 3;
}
if (n > 0)
cout « k « endl;
else
cout << "Не существует";
return 0;
}
|
Последовательно выполните следующее.
1. Напишите, что выведет эта программа при вводе числа 9.
2. Приведите пример числа, при вводе которого приведённая программа напечатает то, что требуется.
3. Найдите в программе все ошибки (их может быть одна или несколько).
Для каждой ошибки выпишите строку, в которой она допущена, и приведите эту же строку в исправленном виде.
Достаточно указать ошибки и способ их исправления для одного языка программирования.
Обратите внимание: Вам нужно исправить приведённую программу, а не написать свою. Вы можете только заменять ошибочные строки, но не можете удалять строки или добавлять новые. Заменять следует только ошибочные строки: за исправления, внесённые в строки, не содержащие ошибок, баллы будут снижаться.
Пояснение
1. При вводе числа 9 программа выведет число 1.
2. Примеры чисел, при вводе которых программа выводит корректный ответ: 2, 3. Других чисел нет.
Комментарий для экспертов. После выполнения программы при любом введённом n значение k будет равно 1 (тело цикла выполнится ровно 1 раз).
В результате программа напечатает либо 1 (если n ≥ 3), либо «Не существует» (в противном случае). Таким образом, программа выводит корректный ответ, только если введено 2 или 3. Экзаменуемому достаточно указать любое из этих чисел. Отметим, что при n=1 программа напечатает «Не существует», что неверно (должно быть напечатано «0»).
3. Программа содержит две ошибки:
1) неверное условие цикла;
2) неверное условие при печати результата.
Пример исправления для языка Паскаль:
Первая ошибка:
while k mod 3 = 0 do begin
Исправленная строка:
while n mod 3 = 0 do begin
Вторая ошибка:
if n>0 then
Исправленная строка:
if n=1 then
Ваш ответ:
Вы пропустили вопрос
Вопрос 25
Дан массив, содержащий 2018 положительных целых чисел, не превышающих 30 000. Необходимо найти в этом массиве количество элементов, которые кратны 7, а их десятичная запись заканчивается цифрой 3, и заменить каждый из таких элементов на это количество.
Напишите на одном из языков программирования программу для решения этой задачи. В качестве результата программа должна вывести изменённый массив, по одному элементу в строке. Например, для исходного массива из 5 элементов 14 13 63 203 49 программа должна вывести числа 14 13 2 2 49, по одному числу в строке.
Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать часть из описанных.
| Бейсик | Python |
|---|
CONST N=2018
DIM A(N) AS INTEGER
DIM I, K, M AS INTEGER
FOR I = 1 TO N
INPUT A(I)
NEXT I
…
END
|
# кроме уже указанных
# допускается использование
# целочисленных переменных
# k, m
a = []
n = 2018
for i in range(0, n):
a.append(int(input()))
…
|
| Паскаль | Алгоритмический язык |
|---|
const
N=2018;
var
a: array [1..N] of integer;
i, k, m: integer;
begin
for i:=1 to N do
readln(a[i]);
…
end.
|
алг
нач
цел N=2018
целтаб a[1:N]
цел i, k, m
нц для i от 1 до N
ввод a[i]
кц
…
кон
|
| С++ |
|---|
#include <iostream>
using namespacestd;
const int N=2018;
int main(){
int a[N];
int i, k, m;
for (i=0; i<N; ++i)
cin >> a[i];
…
return 0;
}
|
Пояснение
Задача решается в два прохода: на первом проходе подсчитывается количество удовлетворяющих условиям элементов, на втором каждый такой элемент заменяется на найденное количество и выводится. Возможно решение в три прохода, когда на втором проходе выполняется только замена значений, а на третьем — вывод.
Пример правильной программы на языке Паскаль:
| Паскаль |
|---|
|
k :=0;
for i:=1 to N do begin
if (a[i] mod 7 = 0) and (a[i] mod 10 = 3)
then k := k + 1;
end;
for i:=1 to N do begin
if (a[i] mod 7 = 0) and (a[i] mod 10 = 3)
then a[i] := k;
writeln(a[i])
end;
|
При использовании языка Python первый проход можно записать в одну строку, используя специальные средства этого языка.
| Python |
|---|
|
k = sum (1 for m in a if m%7 == 0 and m%10 == 3)
for i in range(0, n):
if a[i]%7 == 0 and a[i]%10 == 3:
a[i] = k
print(a[i])
|
Использовать описанную выше возможность не обязательно, на языке Python допустимо описывать развёрнутый алгоритм решения, аналогичный приведённой выше программе на языке Паскаль.
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 33. Если при этом в куче оказалось не более 89 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 30 камней и Паша утроит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1 ≤ S ≤ 32.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания.
1. а) При каких значениях числа S Паша может выиграть в один ход?
Укажите все такие значения и соответствующие ходы Паши.
б) У кого из игроков есть выигрышная стратегия при S = 31; 30; 29?
Опишите выигрышные стратегии для этих случаев.
2. У кого из игроков есть выигрышная стратегия при S = 10; 9? Опишите соответствующие выигрышные стратегии.
3. У кого из игроков есть выигрышная стратегия при S = 8? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в позиции.
Пояснение
1. а) Паша может выиграть, если S = 32 или S = 11; 12; …; 29. При S = 32 первым ходом нужно добавить в кучу 1 камень, при остальных указанных значениях S нужно утроить количество камней.
б) При S = 29 Паша выигрывает в один ход, утраивая количество камней (см. п. а). При S = 30 или 31 утраивать количество камней не имеет смысла, так как после такого хода выигрывает противник.
Поэтому можно считать, что единственный возможный ход — это добавление в кучу одного камня.
При S = 31 после такого хода Паши в куче станет 32 камня. В этой позиции ходящий (т. е. Валя) выигрывает (см. п. а)), т. е. при S = 31 Паша (игрок, который должен ходить первым) проигрывает.
Выигрышная стратегия есть у Вали.
При S = 30, после того как Паша своим первым ходом добавит один камень, в куче станет 31 камень. В этой позиции ходящий (т. е. Валя) проигрывает (см. выше). Т. е., при S = 30 Паша (игрок, который должен ходить первым) выигрывает. Выигрышная стратегия есть у Паши.
Комментарии для экспертов. Скорее всего, решение экзаменуемого будет не столь подробным. Это не является ошибкой. Ученик может, например, нарисовать деревья всех возможных партий для указанных значений S. Другая возможность — (1) указать на то, что при S = 30 и 31 утраивать кучу смысла не имеет, и (2) последовательно сводить случай S = 31 к случаю S = 32, а случай S = 30 — к случаю S = 31.
2. При S = 10 после первого хода Паши в куче будет либо 11, либо 30 камней. В обоих случаях выигрышная стратегия есть у игрока, который должен ходить, теперь это Валя. Случай S = 11 рассмотрен в задании 1(а), а случай S = 30 — в задании 1(б). Поэтому выигрышная стратегия есть у Вали. При S = 9 выигрышная стратегия есть у Паши. Ему нужно первым ходом добавить 1 камень и получить кучу из 10 камней. Как показано выше, в этой ситуации выигрышная стратегия есть у игрока, который НЕ должен ходить, т. е. у Паши.
3. При S = 8 выигрышная стратегия есть у Вали. После первого хода Паши в куче может стать либо 9 камней, либо 24 камня. В обеих этих позициях выигрывает игрок, который будет делать ход (теперь это Валя). Случай S = 9 рассмотрен в п. 2, случай S = 24 рассмотрен в п. 1 а.
В таблице изображено дерево возможных партий при описанной стратегии Вали. Заключительные позиции (в них выигрывает Валя) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).

Ваш ответ:
Вы пропустили вопрос
Вопрос 27
Радиотелескоп пытается получать и анализировать сигналы, поступающие из различных участков космоса, при этом различные шумы переводятся в последовательность целых неотрицательных чисел. Чисел может быть очень много, но не может быть меньше трёх. Все числа различны. Хотя бы одно из чисел нечётно.
В данных, полученных из одного участка, выделяется основное подмножество чисел. Это непустое подмножество чисел (в него могут войти как одно число, так и все поступившие числа), такое, что их сумма нечётна и максимальна среди всех возможных непустых подмножеств с нечётной суммой. Если таких подмножеств несколько, то из них выбирается то подмножество, которое содержит наименьшее количество элементов.
Вам предлагается написать программу (укажите используемую версию языка программирования, например, Borland Pascal 7.0), которая будет обрабатывать результаты, приходящие из одного участка, находя основное подмножество. Перед текстом программы кратко опишите используемый Вами алгоритм решения задачи. На вход программе в первой строке подаётся количество сигналов N. В каждой из последующих N строк записано одно целое неотрицательное число, не превышающее 109.
Вам предлагается два задания, связанных с этой задачей: задание А и задание Б. Вы можете решать оба задания или одно из них по своему выбору. Итоговая оценка выставляется как максимальная из оценок за задания А и Б. Если решение одного из заданий не представлено, то считается, что оценка за это задание — 0 баллов.
Задание Б является усложнённым вариантом задания А, оно содержит дополнительные требования к программе.
А. Напишите на любом языке программирования программу для решения поставленной задачи, в которой входные данные будут запоминаться в массиве, после чего будут проверены все возможные пары элементов. Перед программой укажите версию языка программирования.
Обязательно укажите, что программа является решением задания А. Максимальная оценка за выполнение задания А — 2 балла.
Б. Напишите программу для решения поставленной задачи, которая будет эффективна как по времени, так и по памяти (или хотя бы по одной из этих характеристик). Программа считается эффективной по времени, если время работы программы пропорционально количеству полученных показаний прибора N, т.е. при увеличении N в k раз время работы программы должно увеличиваться не более чем в k раз. Программа считается эффективной по памяти, если размер памяти, использованной в программе для хранения данных, не зависит от числа N и не превышает 1 килобайта.
Перед программой укажите версию языка программирования и кратко опишите использованный алгоритм.
Обязательно укажите, что программа является решением задания Б. Максимальная оценка за правильную программу, эффективную по времени и по памяти, — 4 балла.
Максимальная оценка за правильную программу, эффективную по времени, но неэффективную по памяти, — 3 балла.
Напоминаем! Не забудьте указать, к какому заданию относится каждая из представленных Вами программ.
Пример входных данных:
3
123
0
2
Программа должна вывести в порядке возрастания номера сигналов, которые принадлежат основному подмножеству данного участка. Нумерация элементов последовательности ведётся с единицы. Пример выходных данных для приведённого выше примера входных данных: 1 3.
Пояснение
Основное подмножество состоит из всех значений сигналов, кроме 0, если он встречается, и кроме минимального нечётного значения, если таких значений чётное число.
Программа читает все входные данные один раз, не запоминая все входные данные в массиве, размер которого равен N. Во время чтения данных запоминается номер 0, если он встретится (по условию все значения различны, поэтому 0 встречается не больше одного раза), подсчитывается количество нечётных значений и ищется минимальное из них. После окончания ввода распечатываются все номера, кроме номера 0 и номера минимального нечётного значения, но только в случае, если их количество чётно.
Баллы начисляются только за программу, которая решает задачу хотя бы для одного частного случая. Ниже приведены примеры решения задания на языках Паскаль и Бейсик. Допускаются решения, записанные на других языках программирования.
| Пример правильной и эффективной программы на языке Паскаль: | Пример правильной и эффективной программы на языке Бейсик: |
|---|
var n,i,j,k,c,min,a: longint;
begin
readln(n);
min := 1000000001;
k := 0;
j := 0;
c := 0;
for i := 1 to n do
begin
readln(a);
if a = 0 then j := i;
if a mod 2 <> 0 then
begin
c := c + 1;
if a < min then
begin
min := a;
k := i;
end
end
end;
for i :=1 to n do
if (i <> j) and ((c mod 2 <> 0) or (i <> k)) then
write(i,' ');
end.
|
INPUT n
min = 0
k = 0
j = 0
c = 0
FOR i = 1 TO n
INPUT a
IF a = 0 THEN j = i
IF a MOD 2 <> 0 THEN
c = c + 1
IF (min = 0) OR (a < min) THEN
min = a
k = i
END IF
END IF
NEXT i
FOR i = 1 TO n
IF (i <> j) AND ((c MOD 2 <>0) OR (i <> k)) THEN
PRINT i
NEXT i
END
|
Пример решения задачи A на языке Паскаль.
var
a: array[1..10000] of integer;
min: integer;
N: integer;
sum: integer;
i: integer;
begin
readln(N);
min := 1000000001;
sum := 0;
for i := 1 to N do readln(a[i]);
for i := 1 to N do begin
sum := sum + a[i];
if (a[i] mod 2 <> 0) and (a[i]<min) then<p=""> min := a[i];
end;
if sum mod 2 = 0 then
for i := 1 to N do
if (a[i] <> min) and (a[i]<>0) then write(i, ' ');
if sum mod 2 <> 0 then
for i := 1 to N do
if (a[i]<>0) then write(i, ' ');
end.
Ваш ответ:
Вы пропустили вопрос




