Вопрос №18

18. Равнобедренный треугольник ABC вписан в окружность радиуса R, ∠ABC = α. Параллельно основанию АС проведена средняя линия, продолженная до пересечения с окружностью в точках Р и К.

а) Докажите, что высота треугольника

б) Найдите отношение площади треугольника ABC к площади треугольника КВР, если ∠ABC = 120°.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Равнобедренный треугольник ABC вписан в окружность радиуса R, ∠ABC = α. Параллельно основанию АС проведена средняя линия, продолженная до пересечения с окружностью в точках М и N.

а) Докажите, что 

б) Найдите отношение площади треугольника MBN к площади треугольника ABC, если ∠ABC = 60°.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. В равнобедренную трапецию вписана окружность.

а) Докажите, что диаметр окружности есть среднее пропорциональное между параллельными сторонами.

б) Найдите радиус этой окружности, если площадь трапеции равна 52, а параллельные стороны относятся как 3 : 5.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. К окружности с центром О проведены три касательные, две из которых — АС и BD— параллельны A и В — точки касания. Третья касательная пересекает их в точках С и D соответственно, а также касается окружности в точке F.

а) Докажите, что произведение отрезков касательных, отсекаемых третьей касательной на двух параллельных касательных, равно квадрату радиуса, то есть

АС • BD = АО².

б) Найдите площадь четырёхугольника ABDC, если BD = 12, ∠BDF = 120°.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Диагонали АС и BD трапеции ABCD взаимно перпендикулярны и пересекаются в точке О, причём АО ∙ СО = ВО ∙ DO.

а) Докажите, что трапеция ABCD равнобедренная.

б) Найдите радиус описанной вокруг трапеции окружности, если основания трапеции равны 6 и 8.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Диагонали АС и BD трапеции ABCD взаимно перпендикулярны и пересекаются в точке О, причём АО ∙ СО = BО ∙ DO.

а) Докажите, что средняя линия трапеции равна высоте.

б) Найдите боковую сторону трапеции, если радиус описанной вокруг трапеции окружности равен 3.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Две окружности с центрами О и O₁, радиусы которых относятся как 1: 3, касаются внешним образом, длина их общей внешней касательной АС равна .

а) Докажите, что угол АОО₁ равен 120° (ОА — радиус, проведённый в точку касания).

б) Найдите периметр фигуры, образованной внешними касательными и внешними дугами окружностей.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Две окружности с центрами О и О₁радиусы которых 2 и 6, касаются внешним образом, АС — их общая внешняя касательная.

а) Докажите, что угол СO₁O равен 60°, где O₁С — радиус, проведённый в точку касания.

б) Найдите периметр фигуры, образованной внешними касательными и внешними дугами окружностей.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. В выпуклом пятиугольнике ABCDE диагонали BE и СЕ являются биссектрисами неравных углов при вершинах В и С соответственно.

а) Докажите, что точка Е есть центр вписанной или вневписанной окружности треугольника ОСВ, где О — точка пересечения прямых CD и АВ.

б) Найдите площадь пятиугольника ABCDE, если ∠A = 37°, ∠D = 143°, а площадь треугольника ВСЕ равна 13.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. В выпуклом четырёхугольнике ABCD на сторонах AD и CD взяты точки М и N, такие, что каждая из прямых СМ и AN делит ABCD на две фигуры равных площадей.

а) Докажите, что AC || MN.

б) Найдите отношение площадей четырёхугольников ABCD и ABC О, где О — точка пересечения BD и MN.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Внутри прямого угла АО В проведён луч ОС. В угол ВОС вписана окружность, касающаяся лучей ОВ и ОС в точках В и С соответственно, в угол АОС вписана окружность, касающаяся лучей ОА и ОС в точках А и С соответственно. Радиус одной из этих окружностей в 3 раза больше радиуса другой.

а) Докажите, что если Р и Q — центры этих окружностей, то ∠POQ = 45°.

б) Найдите косинус меньшего из углов АОС и ВОС.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Внутри прямого угла АОВ проведён луч ОС. В угол ВОС вписана окружность, касающаяся лучей ОВ и ОС в точках В и С соответственно, в угол АОС вписана окружность, касающаяся лучей ОА и ОС в точках А и С соответственно. Радиус одной из этих окружностей в 4 раза больше радиуса другой.

а) Докажите, что ОА = ОВ.

б) Найдите косинус меньшего из углов АОС и ВОС.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. В треугольнике ABC высота СН и медиана С К делят угол АС В на три равных угла. Площадь треугольника ABC равна

а) Докажите, что треугольник ABC прямоугольный.

б) Найдите радиус вписанной в треугольник ABC окружности.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. В треугольнике MNP высота PQ и медиана PL делят угол MPN на три равных угла. Площадь треугольника MNP равна .

а) Докажите, что треугольник MNP прямоугольный.

б) Найдите радиус вписанной в треугольник MNP окружности.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Прямая пересекает стороны АВ и ВС треугольника ABC в точках М и N соответственно, а продолжение стороны АС эта прямая пересекает в точке Р.

а) Докажите, что 

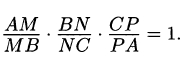
б) Найдите, в каком отношении точка М делит сторону АВ, если ВС : BN = 7 : 5 и АС : СР = 8 : 3.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. На сторонах АВ, ВС и АС треугольника ABC лежат точки М, Р и R соответственно, причём отрезки BR, СМ и АР пересекаются в точке О.

а) Докажите, что 

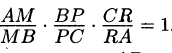
б) Найдите длину стороны АВ, если ВС = 10, АС = 13, ВМ : ВР = 3 : 2,CR = 9.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Радиусы двух окружностей с центрами O₁ и О₂, касающихся внешним образом в точке А, равны 6 и 3 соответственно. Их общая секущая, проведённая через точку А, пересекает первую окружность в точке Б, вторую в точке С.

а) Докажите, что

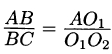
б) Найдите длину касательной, проведённой из точки В ко второй окружности, если дополнительно известно, что АВ = 4.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Радиусы двух окружностей с центрами O₁и О₂, касающихся внутренним образом в точке А, равны 5 и 4 соответственно. Их общая секущая, проведённая через точку А, пересекает первую окружность в точке В, вторую — в точке С.

а) Докажите, что 

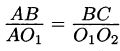
б) Найдите длину касательной, проведённой из точки В ко второй окружности, если дополнительно известно, что АВ = 1.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Биссектриса острого угла А трапеции ABCD пересекает сторону трапеции в точке Т, а продолжение осноавания трапеции ВС точке К так, что ABКD — параллелограмм и ТD : TC = 4.

а) Докажите, что AK перпендикулярна BD.

б) Найдите периметр трапеции ABCD, если её сторона АВ равна 8 и угол В равен 120°.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Биссектриса тупого угла А трапеции ABCD пересекает сторону ВС трапеции в точке Т, а продолжение стороны CD в точке К так, что ABTD — параллелограмм и КС : CD = 2:3.

а) Докажите, что AT перпендикулярна BD.

б) Найдите периметр трапеции ABCD, если её боковая сторона АВ равна 15, а угол В трапеции равен 45°.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос№18

18. В треугольнике ABC известно, что  ∟ВАС = 60°, ∟ABC = 45°. Продолжения высот треугольника ABC пересекают описанную около него окружность в точках М, N, Р.

а) Докажите, что треугольник MNP прямоугольный.
б) Найдите площадь треугольника MNP, если известно, что ВС = 12. 

Ответ на задание находится во вкладке "пяснение",  после выполнения задания сверьте ответ. Если ответ совпадает поставьте знак "+" в поле ответа, если ответ неверен, то поставьте знак "-".

Вопрос№18

18. Прямая, параллельная основаниям ВС и AD трапеции ABCD, пересекает боковые стороны АВ и CD в точках М и N. Диагонали АС и BD пересекаются в точке О. Прямая MN пересекает стороны ОА и OD треугольника AOD в точках К и L соответственно.

а) Докажите, что МК = NL.
б) Найдите MN, если известно, что ВС = 10, AD = 18 и МК : KL = 1:2.

Вопрос№18

18. Диагональ АС прямоугольника ABCD с центром О образует со стороной АВ угол 30°. Точка Е лежит вне прямоугольника, причём ∟BEC = 120°.

а) Докажите, что ∟CBE = ∟COE.
б) Прямая ОЕ пересекает сторону AD прямоугольника в точке К. Найдите ЕК, если известно, что BE = 21 и СЕ = 24.

Вопрос №18

18. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.

а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Прямая, параллельная основаниям ВС и AD трапеции ABCD, пересекает боковые стороны АВ и CD в точках М и N. Диагонали АС и BD пересекаются в точке О. Прямая MN пересекает стороны ОА и OD треугольника AOD в точках К и L соответственно.

а) Докажите, что МК = NL.
б) Найдите MN, если известно, что ВС = 6, AD = 9 и МК : KL =1:2.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Диагональ АС прямоугольника ABCD с центром О образует со стороной АВ угол 30° . Точка Е лежит вне прямоугольника, причём ∠BEC = 120°.

а) Докажите, что  ∠CBE = ∠COE.
б) Прямая ОЕ пересекает сторону AD прямоугольника в точке К. Найдите ЕК, если известно, что BE = 40 и СЕ = 24.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Вневписанная окружность равнобедренного треугольника касается его боковой стороны.

а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в пять раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-". 

Вопрос №18

18. Прямая, параллельная основаниям ВС и AD трапеции ABCD, пересекает боковые стороны АВ и CD в точках М и N. Диагонали АС и BD пересекаются в точке О. Прямая MN пересекает стороны ОА и OD треугольника AOD в точках К и L соответственно.

а) Докажите, что МК = NL.
б) Найдите MN, если известно, что ВС = 3, AD = 8 и МК : KL = 1:3.

Сравните полученный вами ответ с ответом, указанным во вкладке "пояснение". Если ответ правильный, то введите знак "+" в поле ответа, если ответ неверный, то введите знак "-".