Русский язык (Определение главной информации текста)
Результаты теста
Затрачено времени:
15:46:15
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может.
У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится.
Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Выполните задание.
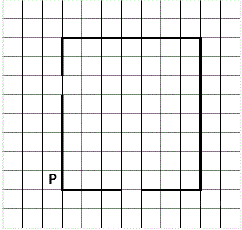

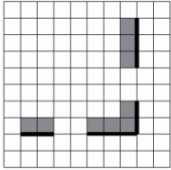
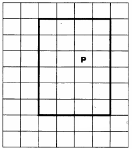
На бесконечном поле имеются четыре стены, соединённые между собой, которые образуют прямоугольник. Длины стен неизвестны. В левой вертикальной стене есть ровно один проход, в нижней горизонтальной стене
также есть ровно один проход. Проход не может примыкать к углу прямоугольника. Точные места проходов и ширина проходов неизвестны. Робот находится около нижнего конца левой вертикальной стены, снаружи прямоугольника и выше нижней стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные вдоль стен прямоугольника с внутренней стороны. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого
расположения стен и любого расположения и размера прохода внутри стены. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе.
20.2 Напишите программу, которая в последовательности натуральных чисел определяет минимальное чётное число.
Программа получает на вход количество чисел в последовательности, а затем сами числа. В последовательности всегда имеется чётное число. Количество чисел не превышает 1000. Введённые числа не превышают 30 000.
Программа должна вывести одно число — минимальное чётное число.
Пример работы программы:
| Входные данные |
Выходные данные |
|
4
3
20
6
8
|
6 |
Пояснение
20.1 Команды исполнителя будем записывать жирным шрифтом, а комментарии, поясняющие алгоритм и не являющиеся его частью, —курсивом. Начало комментария будем обозначать символом «|».
| Двигаемся вверх, пока не дойдём до прохода в стене,
нц пока не справа свободно
вверх
кц
| Через проход входим внутрь прямоугольника
вправо
| Двигаемся вниз до нижней стены, закрашивая все клетки на пути
нц пока снизу свободно
вниз
закрасить
кц
| Двигаемся вправо, вдоль стены до прохода, закрашиваем все клетки на пути
нц пока не снизу свободно
закрасить
вправо
кц
| Двигаемся вправо, пересекаем проход в стене
нц пока снизу свободно
вправо
кц
| Двигаемся вправо, вдоль стены до конца стены, закрашиваем все клетки на пути
нц пока справа свободно
закрасить
вправо
кц
| Двигаемся вверх, вдоль вертикальной стены, закрашиваем все клетки на пути
нц пока сверху свободно
закрасить
вверх
кц
| Двигаемся влево, вдоль верхней горизонтальной стены, закрашиваем все клетки на пути
нц пока слева свободно
закрасить
влево
кц
| Двигаемся вниз, вдоль стены, до прохода в стене, закрашиваем все клетки на пути
нц пока не слева свободно
закрасить
вниз
кц
Возможны и другие варианты решения.
20.2 Решением является программа, записанная на любом языке программирования. Пример верного решения, записанного на языке Паскаль:
var n,i,a,min: integer;
begin
readln(n);
min := 30001;
for i := 1 to n do
begin
readln(a);
if (a mod 2 = 0) and (a < min)
then min:= a;
end;
writeln(min)
end.
Возможны и другие варианты решения. Для проверки правильности работы программы необходимо использовать следующие тесты:
| № |
Входные данные |
Выходные данные |
| 1 |
3
10
4
19
|
4 |
| 2 |
3
11
22
44
|
22 |
| 3 |
3
9
11
2
|
2 |
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Выполните задание.
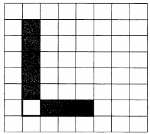
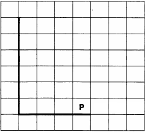
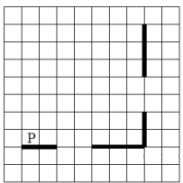
На бесконечном поле имеется вертикальная стена. Длина стены неизвестна. От нижнего конца стены вправо отходит горизонтальная стена также неизвестной длины. Робот находится в клетке, расположенной над правым краем горизонтальной стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены, выше горизонтальной стены и примыкающие к ним, кроме угловой клетки. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
20.2 Напишите программу для решения следующей задачи. Камера наблюдения регистрирует в автоматическом режиме скорость проезжающих мимо неё автомобилей, округляя значения скорости до целых чисел. Необходимо определить среднюю зарегистрированную скорость всех автомобилей. Если скорость хотя бы одного автомобиля была не меньше 60 км/ч, выведите «YES», иначе выведите «NO».
Программа получает на вход число проехавших автомобилей N (1 ≤ N ≤ 30), затем указываются их скорости. Значение скорости не может быть меньше 1 и больше 300. Программа должна сначала вывести среднюю скорость с точностью до одного знака после запятой, затем «YES» или «NO».
Пример работы программы:
| Входные данные |
Выходные данные |
4
74
69
63
96 |
75.5
YES |
Пояснение
1.В ячейку L1 запишем формулу: 100*СЧЁТЕСЛИ(Е2: Е1001;" <5 ")/1000. Таким образом, мы найдём отношение количества тех, кто пробежал меньше, чем за 5 минут, к общему числу участников в процентах. Множитель «100» необходим как раз для того, чтобы получилось отношение не в долях от единицы, а в процентах.
2. Для ответа на второй вопрос в столбце Н выпишем все результаты девочек по прыжкам в длину при помощи формулы: =ЕСЛИ(C2="ж";G2;""). Скопируем формулу во все ячейки диапазона НЗ:Н1001. Найдём среднее значение по прыжкам в длину среди девочек по формуле =СРЗНАЧ(Н2:Н1001) запишем его в ячейку J1, получим 201,83. Аналогично поступим с мальчиками. Результаты мальчиков выпишем в столбце I =ЕСЛИ(C2="м";G2;""). Скопируем формулу во все ячейки диапазона I3:I1001. Среднее значение среди мальчиков запишем в J2:=СРЗНАЧ(I2:I1001), получим 208,19. В ячейку L2 запишем разницу между J2 и J1 =J2-J1 Зададим формат ячейки L2 числовой, число десятичных знаков — 1.
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может.
У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится.
Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц

Выполните задание.
Робот находится в левой клетке узкого горизонтального коридора. Ширина коридора — одна клетка, длина коридора может быть произвольной. Возможный вариант начального расположения Робота приведён на рисунке (Робот обозначен буквой «Р»):
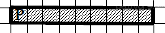
Напишите для Робота алгоритм, закрашивающий все клетки внутри коридора и возвращающий Робота в исходную позицию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок). Алгоритм должен решать задачу для произвольного конечного размера коридора. При исполнении алгоритма Робот не должен разрушиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе.
20.2 Напишите программу, которая в последовательности натуральных чисел определяет количество чисел, кратных 6 и оканчивающихся на 4. Программа получает на вход количество чисел в последовательности, а затем сами числа. Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести одно число: количество чисел, кратных 6 и оканчивающихся на 4.
Пример работы программы:
| Входные данные |
Выходные данные |
|
3
24
25
54
|
2
|
Пояснение
20.1 Команды исполнителя будем записывать жирным шрифтом, а комментарии, поясняющие алгоритм и не являющиеся его частью, — курсивом. Начало комментария будем обозначать символом «|».
|Сначала будем двигаться направо и закрашивать клетки, пока не дойдём до конца коридора.
нц пока справа свободно
закрасить
вправо
кц
|Закрасим последнюю клетку.
закрасить
|Теперь вернёмся в исходную клетку.
нц пока слева свободно
влево
кц
Возможны и другие варианты решения. Допускается использование иного синтаксиса инструкций исполнителя, более привычного для учащихся. Допускается наличие отдельных синтаксических ошибок, не искажающих замысла автора решения
20.2 Решением является программа, записанная на любом языке программирования. Пример верного решения, записанного на языке Паскаль:
var i, n, a, s: integer;
begin
s := 0;
readln(n);
for i:=1 to n do
begin
readln(a);
if (a mod 6=0) and (a mod 10 = 4) then
s := s + 1;
end;
writeln(s);
end.
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Выполните задание.
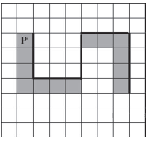
На бесконечном поле есть горизонтальная и вертикальная стены. Правый конец горизонтальной стены соединён с нижним концом вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно над горизонтальной стеной у её левого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно выше горизонтальной стены и левее вертикальной стены. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
20.2 Напишите программу, которая в последовательности натуральных чисел определяет сумму чисел, кратных 6. Программа получает на вход количество чисел в последовательности, а затем сами числа. В последовательности всегда имеется число, кратное 6. Количество чисел не превышает 100. Введённые числа не превышают 300. Программа должна вывести одно число — сумму чисел, кратных 6.
Пример работы программы:
| Входные данные |
Выходные данные |
3
12
25
6 |
18 |
Пояснение
20.1 Следующий алгоритм выполнит требуемую задачу.
нц
пока не снизу свободно
закрасить
вправо
кц
нц
пока снизу свободно
вправо
кц
нц
пока справа свободно
закрасить
вправо
кц
нц
пока не справа свободно
закрасить
вверх
кц
нц
пока справа свободно
вверх
кц
нц
пока не справа свободно
закрасить
вверх
кц
20.2 Решение
var n, s, k, g: integer;
begin
s:=0;
readln(n);
for k:=1 to n do
begin
readln(g);
if (g mod 6 = 0) then
s:=s+g;
end;
writeln(s);
end.
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Выполните задание.
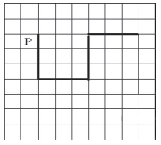
На бесконечном поле имеется стена, состоящая из 5 последовательных отрезков, расположенных змейкой: вниз, вправо, вверх, вправо, вниз. Все отрезки неизвестной длины. Робот находится в клетке, расположенной слева от верхнего края первой вертикальной стены. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные левее первого и ниже второго отрезков стены и ниже четвёртого и левее пятого отрезков стены. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
20.2 Напишите программу, которая в последовательности натуральных чисел определяет сумму всех чисел, кратных 3 и оканчивающихся на 4. Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 — признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введённые числа не превышают 30000. Программа должна вывести одно число: сумму всех натуральных чисел, кратных 3 и оканчивающихся на 4.
Пример работы программы:
| Входные данные |
Выходные данные |
16
24
56
22
54
0 |
78 |
Пояснение
Следующий алгоритм выполнит требуемую задачу.
нц
пока не справа свободно
закрасить
вниз
кц
закрасить
вправо
нц
пока не сверху свободно
закрасить
вправо
кц
нц
пока сверху свободно
вверх
кц
нц
пока справа свободно
закрасить
вправо
кц
нц
пока не справа свободно
закрасить
вниз
кц
20.2 Решение
var a, s: integer;
begin
s : = 0;
readln(a);
while a<>0 do begin
if (a mod 3=0) and (a mod 10 = 4) then
s : = s + a;
readln(a);
end;
writeln(s)
end.
Для проверки правильности работы программы необходимо использовать следующие тесты:
| | Входные данные | Выходные данные |
|---|
| 1 |
6
14
10
0
|
0 |
| 2 |
24
0
|
24 |
| 3 |
54
84
5
0
|
138 |
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Выполните задание.

На бесконечном поле имеется прямоугольник, ограниченный стенами. Длины сторон прямоугольника неизвестны. Робот находится внутри прямоугольника. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
Напишите для Робота алгоритм, закрашивающий клетки прямоугольника, примыкающие к его нижней и левой стенам. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
20.2 Напишите программу, которая в последовательности целых чисел определяет их количество и сумму чётных чисел. Программа получает на вход целые числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 — признак окончания ввода, не входит в последовательность).
Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести два числа: длину последовательности и сумму чётных чисел.
Пояснение
20.1 Следующий алгоритм выполнит требуемую задачу.
нц
пока слева свободно
влево
кц
нц
пока сверху свободно
вверх
кц
нц пока снизу свободно
закрасить
вниз
кц
закрасить
нц пока справа свободно
закрасить
вправо
кц
закрасить
20.2 Решение
var N, a, sum: integer;
begin
sum := 0;N := 0; readln(a); while a <> 0 do begin
N := N + 1;
if (a mod 2=0) then sum := sum + a; readln(a);
end;
writeln(N); writeln(sum)
end.
Для проверки правильности работы программы необходимо использовать следующие тесты:
| | Входные данные | Выходные данные |
|---|
| 1 |
1
20
21
30
0
|
4
50
|
| 2 |
10
0
|
1
10
|
| 3 |
101
29
0
|
2
0
|
| 4 |
45
1000
20
0
|
3
1020
|
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может.
У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится.
Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц

Выполните задание.
Робот находится в правой клетке узкого горизонтального коридора. Ширина коридора — одна клетка, длина коридора может быть произвольной. Возможный вариант начального расположения Робота приведён на рисунке (Робот обозначен буквой «Р»):

Напишите для Робота алгоритм, закрашивающий все клетки внутри коридора и возвращающий Робота в исходную позицию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок). Алгоритм должен решать задачу для произвольного конечного размера коридора. При исполнении алгоритма Робот не должен разрушиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе.
20.2 Напишите программу, которая в последовательности натуральных чисел определяет количество трёхзначных чисел, кратных 4. Программа получает на вход натуральные числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 — признак окончания ввода, не входит в последовательность).
Количество чисел не превышает 1000. Введённые числа не превышают 30 000. Программа должна вывести одно число: количество трёхзначных чисел, кратных 4.
Пример работы программы:
| Входные данные |
Выходные данные |
|
120
9
365
4
0
|
1
|
Пояснение
20.1 Команды исполнителя будем записывать жирным шрифтом, а комментарии, поясняющие алгоритм и не являющиеся его частью, — курсивом. Начало комментария будем обозначать символом «|».
|Закрасим начальную клетку
закрасить
|Двигаемся влево, пока не дойдём до конца коридора, закрашивая все клетки на пути
нц пока слева свободно
влево
закрасить
кц
|Двигаемся вправо, возвращаясь в начальную клетку
нц пока справа свободно
вправо
кц
Возможны и другие варианты решения. Допускается использование иного синтаксиса инструкций исполнителя,
более привычного для учащихся. Допускается наличие отдельных синтаксических ошибок, не искажающих замысла автора решения
20.2 Решением является программа, записанная на любом языке программирования. Пример верного решения, записанного на языке Паскаль:
var a, answer: integer;
begin
answer:=0;
readln(a);
while a<>0 do begin
if (a mod 4 = 0) and (a > 99) and (a <1000) then
answer := answer + 1;
readln(a); end;
writeln(answer)
end.
Возможны и другие варианты решения.
Для проверки правильности работы программы необходимо использовать следующие тесты:
| № | Входные данные | Выходные данные |
|---|
| 1 |
300
16
17
0
|
1 |
| 2 |
1000
8
0
|
0 |
| 3 |
400
420
0
|
2 |
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «eсли», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов.
Например, для передвижения на одну клетку вправо, если справа нет стенки и закрашивания клетки, можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не, например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Выполните задание.
На бесконечном поле имеются две вертикальные стены и одна горизонтальная, соединяющая нижний конец левой и верхний конец правой вертикальных стен. Длины стен неизвестны. Робот находится в клетке, расположенной слева от нижнего края правой вертикальной стены, рядом со стеной. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
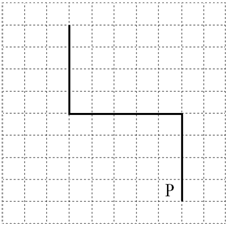
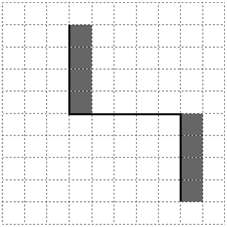
Напишите для Робота алгоритм, закрашивающий все клетки, примыкающие к вертикальным стенам справа. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в формате программы Кумир или в текстовом файле. Название файла и каталог для сохранения Вам сообщат организаторы экзамена.
20.2 Напишите программу для решения следующей задачи. Ученики 4 класса вели дневники наблюдения за погодой и ежедневно записывали дневную температуру. Найдите среднюю температуру за время наблюдения. Если количество дней, когда температура поднималась выше нуля градусов, не менее 5, выведите YES, иначе выведите NO. Программа получает на вход количество дней, в течение которых проводилось наблюдение N (1 ≤ N ≤ 31), затем для каждого дня вводится температура.
Пример работы программы:
|
Входные данные
|
Выходные данные
|
|
4
−4
12
−2
8
|
3.5
NO
|
Пояснение
20.1 Следующий алгоритм выполнит требуемую задачу.
нц пока не справа свободно
вниз
кц
вправо
нц пока слева свободно
вверх
кц
нц пока не слева свободно
закрасить
вверх
кц
нц пока слева свободно
влево
кц
нц пока не слева свободно
закрасить
вверх
кц
20.2 Решением является программа, записанная на любом языке программирования. Пример верного решения, записанного на языке Паскаль:
var
a, N, i, num : integer;
sredn : real;
begin
num:=0; sredn:=0;
readln(N);
for i:=1 to N do begin
readln(a);
sredn := sredn + a;
if a > 0 then num := num + 1;
end;
sredn := sredn / N;
writeln(sredn);
if num >= 5 then writeln('YES')
else writeln('NO')
end.
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может.
У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится.
Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц

Выполните задание.
Робот находится в левой клетке узкого горизонтального коридора. Ширина коридора — одна клетка, длина коридора может быть произвольной. Возможный вариант начального расположения Робота приведён на рисунке (Робот обозначен буквой «Р»):
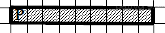
Напишите для Робота алгоритм, закрашивающий все клетки внутри коридора и возвращающий Робота в исходную позицию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок). Алгоритм должен решать задачу для произвольного конечного размера коридора. При исполнении алгоритма Робот не должен разрушиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе.
20.2 Напишите программу, которая в последовательности натуральных чисел определяет количество чисел, кратных 6 и оканчивающихся на 4. Программа получает на вход количество чисел в последовательности, а затем сами числа. Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести одно число: количество чисел, кратных 6 и оканчивающихся на 4.
Пример работы программы:
| Входные данные |
Выходные данные |
|
3
24
25
54
|
2
|
Пояснение
20.1 Команды исполнителя будем записывать жирным шрифтом, а комментарии, поясняющие алгоритм и не являющиеся его частью, — курсивом. Начало комментария будем обозначать символом «|».
|Сначала будем двигаться направо и закрашивать клетки, пока не дойдём до конца коридора.
нц пока справа свободно
закрасить
вправо
кц
|Закрасим последнюю клетку.
закрасить
|Теперь вернёмся в исходную клетку.
нц пока слева свободно
влево
кц
Возможны и другие варианты решения. Допускается использование иного синтаксиса инструкций исполнителя, более привычного для учащихся. Допускается наличие отдельных синтаксических ошибок, не искажающих замысла автора решения
20.2 Решением является программа, записанная на любом языке программирования. Пример верного решения, записанного на языке Паскаль:
var i, n, a, s: integer;
begin
s := 0;
readln(n);
for i:=1 to n do
begin
readln(a);
if (a mod 6=0) and (a mod 10 = 4) then
s := s + 1;
end;
writeln(s);
end.
Ваш ответ:
Вы пропустили вопрос
Вопрос 20
Выберите ОДНО из предложенных ниже заданий: 20.1 или 20.2.
20.1 Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может. У Робота есть девять команд. Четыре команды — это команды-приказы:
вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх ↑ вниз ↓, влево ← , вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится. Также у Робота есть команда закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.
Ещё четыре команды — это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:
сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если», имеющим следующий вид:
если условие то
последовательность команд
все
Здесь условие — одна из команд проверки условия. Последовательность команд — это одна или несколько любых команд-приказов. Например, для передвижения на одну клетку вправо, если справа нет стенки, и закрашивания клетки можно использовать такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не,например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Выполните задание.
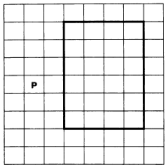
На бесконечном поле имеется прямоугольник, ограниченный стенами. Длины сторон прямоугольника неизвестны. Робот находится слева от прямоугольника. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).
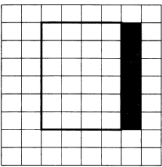
Напишите для Робота алгоритм, закрашивающий клетки снаружи прямоугольника, примыкающие стороной к его правой стене. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.
20.2 Напишите программу, которая в последовательности целых чисел определяет их сумму и подсчитывает разность количества положительных и отрицательных чисел последовательности. Программа получает на вход целые числа, количество введённых чисел неизвестно, последовательность чисел заканчивается числом 0 (0 — признак окончания ввода, не входит в последовательность).
Количество чисел не превышает 1000. Введённые числа по модулю не превышают 30 000. Программа должна вывести два числа: сумму чисел и разность количества положительных и отрицательных чисел.
Пример работы программы:
| Входные данные |
Выходные данные |
150
−200
−1
0 |
−51
−1 |
Пояснение
20.1 Следующий алгоритм выполнит требуемую задачу.
нц
пока справа свободно
вправо
кц
нц
пока не справа свободно
вверх
кц
вправо
нц
пока не снизу свободно
вправо
кц
вниз
нц пока не слева свободно
закрасить
вниз
кц
20.2 Решение
var a, sum, npos, nneg: integer; begin
sum := 0; npos := 0; nneg := 0; readln(a); while a <> 0 do begin
sum := sum + a;
if (a < 0) then nneg := nneg + 1 else npos := npos + 1; readln(a);
end;
writeln(sum); writeln (npos - nneg)
end.
Для проверки правильности работы программы необходимо использовать следующие тесты:
| | Входные данные | Выходные данные |
|---|
| 1 |
1
2
3
0
|
6
3
|
| 2 |
10
0
|
10
1
|
| 3 |
−5
15
0
|
10
0
|
| 4 |
−2000
−3000
0
|
−5000
−2
|
Ваш ответ:
Вы пропустили вопрос















