Русский язык (Определение главной информации текста)
Результаты теста
Затрачено времени:
16:40:38
Вопрос 11
На рисунке — схема дорог, связывающих города A, B, C, D, E, F, G. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город G?
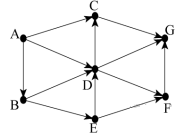
Пояснение
Начнем считать количество путей с конца маршрута — с города G. Пусть NX — количество различных путей из города А в город X, N — общее число путей. В город G можно приехать из C, D или F, поэтому N = NG = NC + ND + NF(*).
Аналогично:
NC = NA + ND = 1 + 3 = 4;
ND = NA + NB + NE = 1 + 1 + 1 = 3;
NF = ND + NE = 3 + 1 = 4;
NB = NA = 1;
NE = NВ = 1.
Подставим в формулу (*): N = 4 + 3 + 4 = 11.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город H?
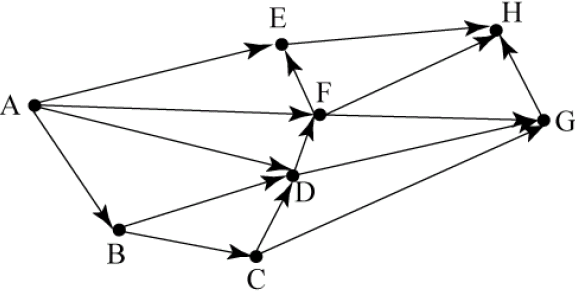
Пояснение
Начнем считать количество путей с конца маршрута — с города H. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В H можно приехать из E, F или G, поэтому N = NH = NE + NF + NG(*).
Аналогично:
NE = NA + NF = 1 + 4 = 5;
NG = NF + ND + NC = 4 + 3 + 1 = 8;
NF = NA + ND = 1 + 3 = 4;
ND = NA + NB + NC = 1+ 1 + 1 = 3;
NC = NB = 1;
NB = NA = 1.
Подставим в формулу (*): N = 5 + 4 + 8 = 17.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
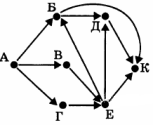
Пояснение
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, Б или Д, поэтому N = NК = NЕ + NБ + NД(*).
Аналогично:
NБ = NА + NЕ = 1 + 2 = 3;
NД = NБ + NЕ = 3 + 2 = 5;
NЕ = NВ + NГ = 1 + 1 = 2;
NВ = NА = 1;
NГ = NА = 1.
Подставим в формулу (*): N = 3 + 5 + 2 = 10.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
На рисунке – схема дорог, связывающих города A, B, C, D, E, F, G, H. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город H?
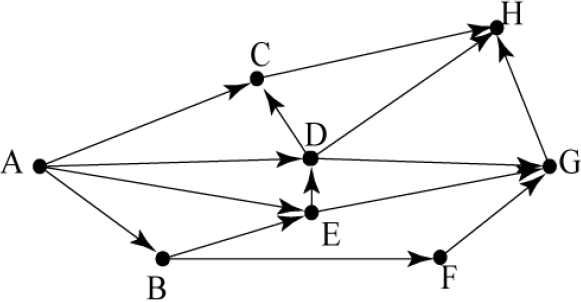
Пояснение
Начнем считать количество путей с конца маршрута — с города H. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В H можно приехать из C, D или G, поэтому N = NH = NC + ND + NG(*).
Аналогично:
NC = NA + ND = 1 + 3 = 4;
NG = ND + NE + NF = 3 + 2 + 1 = 6;
ND = NA + NE = 1 + 2 = 3;
NE = NA + NB = 1 + 1 = 2;
NF = NB = 1;
NB = NA = 1.
Подставим в формулу (*): N = 4 + 3 + 6 = 13.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
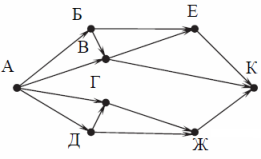
Пояснение
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, или Ж, поэтому N = NК = NЕ + NВ + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 2 = 3;
NВ = NА + NБ = 1 + 1 = 2;
NЖ = NГ + NД = 2 + 1 = 3;
NБ = NА = 1;
NГ = NА + NД = 1 + 1 = 2;
NД = NА = 1.
Подставим в формулу (*): N = 3 + 2 + 3 = 8.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
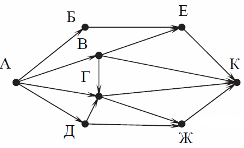
Пояснение
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + NГ + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 1 = 2;
NВ = NА = 1;
NГ = NВ + NА + NД = 1 + 1 + 1 = 3;
NЖ = NГ + NД = 3 + 1 = 4;
NБ = NА = 1;
NД = NА = 1.
Подставим в формулу (*): N = 2 + 1 + 3 + 4 = 10.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
На рисунке — схема дорог, связывающих города A, B, C, D, E, F, G, H, I, J. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город J?
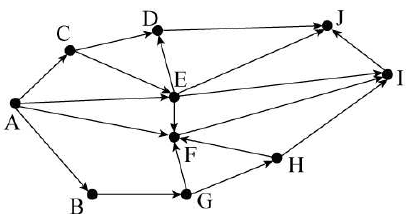
Пояснение
Начнем считать количество путей с конца маршрута — с города J. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В J можно приехать из D, E или I, поэтому N = NJ = ND + NE + NI(*).
Аналогично:
ND = NC + NE = 1 + 2 = 3;
NE = NC + NA = 1 + 1 = 2;
NI = NE + NF + NH = 2 + 5 + 1 = 8;
NC = NA= 1;
NF = NE + NA + NG + NH = 2 + 1 + 1 + 1 = 5;
NH = NG = 1;
NG = NB = 1;
NB = NA = 1.
Подставим в формулу (*): N = 3 + 2 + 8 = 13.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К и Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?
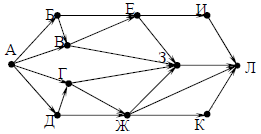
Пояснение
Начнем считать количество путей с конца маршрута — с города Л. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В Л можно приехать из И, З, Ж или К, поэтому N = NЛ = NИ + NЗ + NЖ + NК.
Аналогично:
NИ = NЕ = 3;
NЕ = NБ + NВ = 1 + 2 = 3;
NЗ = NЕ + NВ + NГ + NЖ = 3 + 2 + 2 + 3 = 10;
NЖ = NГ + NД = 2 + 1 = 3;
NК = NЖ = 3;
NБ = NА = 1;
NВ = NA + NБ = 1 + 1 = 2;
NГ = NA + NД = 1 + 1 = 2;
NД = NA = 1;
NA = 1.
Подставим в формулу (*): N = 3 + 10 + 3 + 3 = 19.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
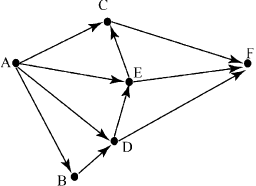
На рисунке изображена схема соединений, связывающих пункты А, В, С, D, Е, F. По каждому соединению можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт F?
Пояснение
Начнем считать количество путей с конца маршрута — с города F. Пусть NX — количество различных путей из города F в город X, N — общее число путей.
В F можно приехать из C или E или D, поэтому N = NF = NC + NE + ND (*).
Аналогично:
NC = NA + NE = 1 + 3 = 4;
NE = NA + ND = 1 + 2 = 3;
ND = NA + NB = 1 + 1 = 2;
NB = NA = 1;
Подставим в формулу (*): N = 4 + 3 + 2 = 9.
Ваш ответ:
Вы пропустили вопрос
Вопрос 11
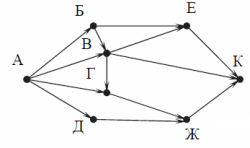
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Пояснение
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.
В К можно приехать из Е, В или Ж, поэтому N = NК = NЕ + NВ + NЖ (*).
Аналогично:
NЕ = NБ + NВ = 1 + 2 = 3;
NВ = NБ + NА = 1 + 1 = 2;
NЖ = NГ + NД = 3 + 1 = 4;
NГ = NА + NВ = 1 + 2 = 3;
NД = NА = 1;
NБ = NА = 1.
Подставим в формулу (*): N = 3 + 2 + 4 = 9.
Ваш ответ:
Вы пропустили вопрос











