Русский язык (Определение главной информации текста)
Результаты теста
Затрачено времени:
08:44:46
Вопрос 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в шесть раз. Например, имея кучу из 10 камней, за один ход можно получить кучу из 11 или 60 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче превышает 365. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 366 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 365.
Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
1. а) При каких значениях числа S Петя может выиграть первым ходом? Укажите все такие значения и выигрывающий ход Пети.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
2. Укажите два значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть первым ходом, но (б) Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.
Для указанных значений S опишите выигрышную стратегию Пети.
3. Укажите такое значение S, при котором
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения Sопишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход, в узлах — количество камней в позиции.
Пояснение
1. а) Петя может выиграть, если S = 61, …, 365. При меньших значениях S за один ход нельзя получить кучу, в которой больше 365 камней. Пете достаточно увеличить количество камней в 6 раз. При S < 61 получить за один ход больше 365 камней невозможно.
б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 60 камней. Тогда после первого хода Пети в куче будет 61 камень или 360 камней. В обоих случаях Ваня увеличивает количество камней в 6 раз и выигрывает в один ход.
2. Возможные значения S: 10, 59. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 60 камней (при S = 10 он увеличивает количество камней в 6 раз; при S = 59 — добавляет 1 камень). Эта позиция разобрана в п. 1б. В ней игрок, который будет ходить (в данном случае это Ваня), выиграть не может, а его противник (то есть, Петя) следующим ходом выиграет.
3. Возможное значение S: 58. После первого хода Пети в куче будет 59 или 348 камней. Если в куче станет 348 камней, Ваня увеличит количество камней в 6 раз и выиграет своим первым ходом. Ситуация, когда в куче 59 камней, разобрана в п. 2. В этой ситуации игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.
В таблице изображено дерево возможных партий при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).
| |
Положения после очередных ходов |
| И.п. |
1-й ход Пети (разобраны все ходы) |
1-й ход Вани (только ход по стратегии) |
2-й ход Пети (разобраны все ходы) |
2-й ход Вани (только ход по стратегии) |
| 58 |
58 + 1 = 59 |
59 + 1 = 60 |
60 + 1 = 61 |
61*6 = 366 |
| 60*6 = 360 |
360*6 = 2160 |
| 58*6 = 348 |
348*6 = 2088 |
|
|
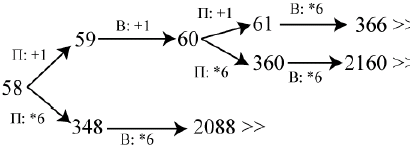
Дерево всех партий, возможных при Ваниной стратегии.
Знаком >> обозначены позиции, в которых партия заканчивается
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 24. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 24 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 23.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
1. а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход и (б) Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети.
3. Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в куче.
Пояснение
1. а) Петя может выиграть, если S=12, ..., 23. Во всех этих случаях достаточно удвоить количество камней. При меньших значениях S за один ход нельзя получить кучу, в которой больше 23 камней.
б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 11 камень. Тогда после первого хода Пети в куче будет 12, 13 или 22 камня. Во всех случаях Ваня удваивает количество камней и выигрывает первым ходом.
2. Возможные значения S: 9, 10. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 11 камней: в первом случае добавлением двух камней, во втором добавлением одного камня. Эта позиция разобрана в п. 16. В ней отрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (то есть Петя) следующим ходом выиграет.
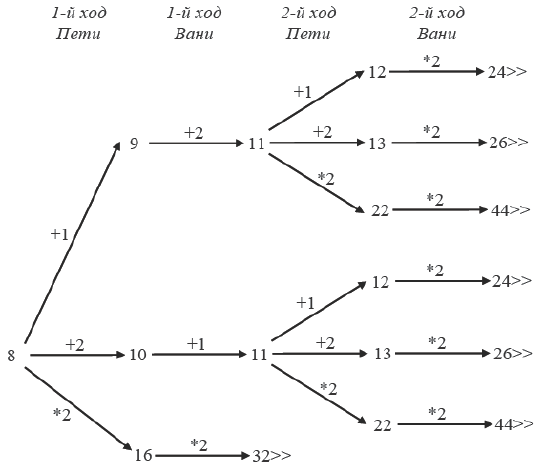
3. Возможное значение S: 8. После первого хода Пети в куче будет 9, 10 или 16 камней. Если в куче станет 16 камней. Ваня удвоит количество камней и выиграет первым ходом. Ситуация, когда в куче 9 или 10 камней, уже разобрана в п. 2. В этих ситуациях игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.
В таблице изображено дерево возможных партий при описанной стратегии Ванн. Заключительные позиции (в них выигрывает Ваня) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).

Указания по оцениванию.
В задаче от ученика требуется выполнить три задания. Их трудность возрастает. Количество баллов в целом соответствует количеству выполненных задании (подробнее см. ниже). Ошибка в решении, не искажающая основного замысла и не приведшая к неверному ответу, например арифметическая ошибка при вычислении количества камней в заключительной позиции, при оценке решения не учитывается.
Первое задание считается выполненным полностью, если выполнены полностью оба пункта: а) и б). Пункт а) считается выполненным полностью, если правильно указаны все позиции, в которых Петя выигрывает первым ходом, и указано, каким должен быть первый ход. Пункт б) считается выполненным полностью, если правильно указана позиция, в которой Ваня выигрывает первым ходом, и описана стратегия Ванн, то есть показано, как Ваня может получить кучу, в которой содержится нужное количество камней, при любом ходе Пети.
Первое задание считается выполненным частично, если: а) правильно указаны все позиции, в которых Петя выигрывает первым ходом; б) правильно указана позиция, в которой Ваня выигрывает первым ходом, и явно сказано, что при любом ходе Пети Ваня может получить кучу, которая содержит нужное для выигрыша количество камней. Отличие от выполненного полностью задания состоит в том. что не указаны явно ходы, которыми выиграет Петя или Ваня.
Второе задание выполнено, если правильно указаны обе позиции, выигрышные для Пети, и описана соответствующая стратегия Пети - так, как это написано в примере решения, или другим способом, например с помощью дерева всех партий, возможных при выбранной стратегии Пети.
Третье задание выполнено, если правильно указана позиция, выигрышная для Ванн, и построено дерево всех партий, возможных при Васиной стратегии. Должно быть явно сказано, что в этом дереве в каждой позиции, где должен ходить Петя, разобраны все возможные ходы, а для позиций, где должен ходить Ваня, — только ход. соответствующий стратегии, которую выбрал Ваня.
Во всех случаях стратегии могут быть описаны так. как это сделано в примере решения или другим способом.
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 33. Если при этом в куче оказалось не более 89 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 30 камней и Паша утроит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1 ≤ S ≤ 32.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания.
1. а) При каких значениях числа S Паша может выиграть в один ход?
Укажите все такие значения и соответствующие ходы Паши.
б) У кого из игроков есть выигрышная стратегия при S = 31; 30; 29?
Опишите выигрышные стратегии для этих случаев.
2. У кого из игроков есть выигрышная стратегия при S = 10; 9? Опишите соответствующие выигрышные стратегии.
3. У кого из игроков есть выигрышная стратегия при S = 8? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в позиции.
Пояснение
1. а) Паша может выиграть, если S = 32 или S = 11; 12; …; 29. При S = 32 первым ходом нужно добавить в кучу 1 камень, при остальных указанных значениях S нужно утроить количество камней.
б) При S = 29 Паша выигрывает в один ход, утраивая количество камней (см. п. а). При S = 30 или 31 утраивать количество камней не имеет смысла, так как после такого хода выигрывает противник.
Поэтому можно считать, что единственный возможный ход — это добавление в кучу одного камня.
При S = 31 после такого хода Паши в куче станет 32 камня. В этой позиции ходящий (т. е. Валя) выигрывает (см. п. а)), т. е. при S = 31 Паша (игрок, который должен ходить первым) проигрывает.
Выигрышная стратегия есть у Вали.
При S = 30, после того как Паша своим первым ходом добавит один камень, в куче станет 31 камень. В этой позиции ходящий (т. е. Валя) проигрывает (см. выше). Т. е., при S = 30 Паша (игрок, который должен ходить первым) выигрывает. Выигрышная стратегия есть у Паши.
Комментарии для экспертов. Скорее всего, решение экзаменуемого будет не столь подробным. Это не является ошибкой. Ученик может, например, нарисовать деревья всех возможных партий для указанных значений S. Другая возможность — (1) указать на то, что при S = 30 и 31 утраивать кучу смысла не имеет, и (2) последовательно сводить случай S = 31 к случаю S = 32, а случай S = 30 — к случаю S = 31.
2. При S = 10 после первого хода Паши в куче будет либо 11, либо 30 камней. В обоих случаях выигрышная стратегия есть у игрока, который должен ходить, теперь это Валя. Случай S = 11 рассмотрен в задании 1(а), а случай S = 30 — в задании 1(б). Поэтому выигрышная стратегия есть у Вали. При S = 9 выигрышная стратегия есть у Паши. Ему нужно первым ходом добавить 1 камень и получить кучу из 10 камней. Как показано выше, в этой ситуации выигрышная стратегия есть у игрока, который НЕ должен ходить, т. е. у Паши.
3. При S = 8 выигрышная стратегия есть у Вали. После первого хода Паши в куче может стать либо 9 камней, либо 24 камня. В обеих этих позициях выигрывает игрок, который будет делать ход (теперь это Валя). Случай S = 9 рассмотрен в п. 2, случай S = 24 рассмотрен в п. 1 а.
В таблице изображено дерево возможных партий при описанной стратегии Вали. Заключительные позиции (в них выигрывает Валя) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).

Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 45 камней. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 51. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 51 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 50.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
Задание 1. а) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б) Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.
Задание 2. Укажите два таких значения S, при которых у Паши есть выигрышная стратегия, причём (а) Паша не может выиграть за один ход и (б) Паша может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.
Задание 3. Укажите значение S, при котором:
— у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и
— у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах – количество камней в
Пояснение
Задание 1.
а) Паша может выиграть, если S = 17, … 50. Во всех этих случаях достаточно утроить количество камней. При меньших значениях S за один ход нельзя получить кучу, в которой больше 50 камней.
б) Вася может выиграть первым ходом (как бы ни играл Паша), если исходно в куче будет S = 16 камня. Тогда после первого хода Паши в куче будет 17, 18 или 48 камней. Во всех случаях Вася утраивает количество камней и выигрывает в один ход.
Задание 2.
Возможные значения S: 14, 15. В этих случаях Паша, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 16 камней: в первом случае добавлением одного камня, во втором — добавлением двух камней. Эта позиция разобрана в п. 1б. В ней игрок, который будет ходить (теперь это Вася), выиграть не может, а его противник (то есть Паша) следующим ходом выиграет.
Задание 3.
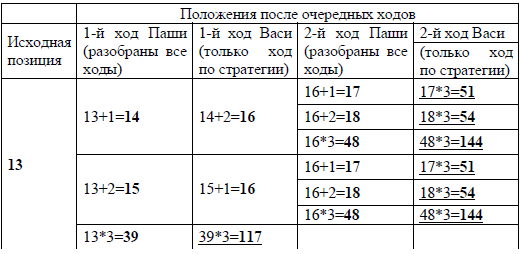
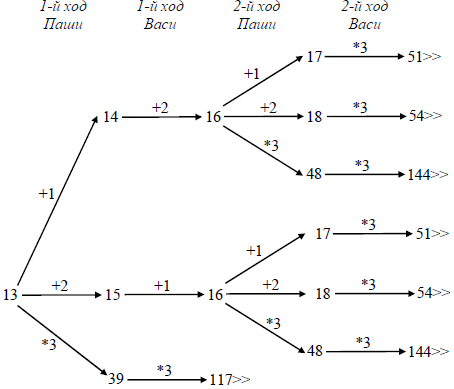
Возможное значение S: 13. После первого хода Паши в куче будет 14, 15 или 39 камней. Если в куче станет 39 камней, Вася утроит количество камней и выиграет первым ходом. Ситуация, когда в куче 14 или 15 камней, разобрана в п. 2. В этих ситуациях игрок, который будет ходить (теперь это Вася), выигрывает своим вторым ходом.
В таблице приведены возможные партии при описанной стратегии Васи. Заключительные позиции (в них выигрывает Вася) подчёркнуты. На рисунке дерево изображено в графическом виде (оба способа изображения дерева допустимы).
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 44. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 44 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 43.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
1. а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход и (б) Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети.
3. Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в куче.
Пояснение
1. а) Петя может выиграть, если S = 22, ... 43. Во всех этих случаях достаточно удвоить количество камней. При меньших значениях S за один ход нельзя получить кучу, в которой больше 43 камней.
б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 21 камней. Тогда после первого хода Пети в куче будет 22, 23 или 42 камня. Во всех случаях Ваня удваивает количество камней и выигрывает первым ходом.
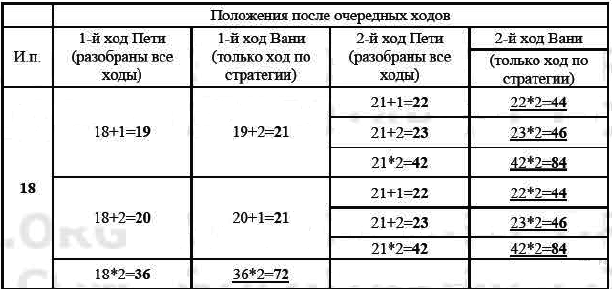
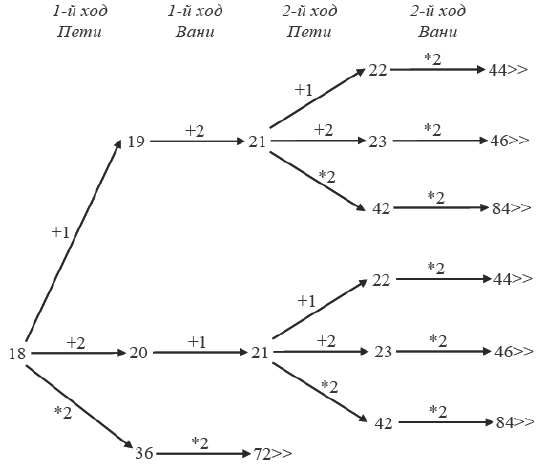
2. Возможные значения S: 19, 20. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 21 камня: в первом случае добавлением двух камней, во втором добавлением одного камня. Эта позиция разобрана в п. 16. В ней отрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (то есть Петя) следующим ходом выиграет.
3. Возможное значение S: 18. После первого хода Пети в куче будет 19, 20 или 36 камней. Если в куче станет 38 камней. Ваня удвоит количество камней и выиграет первым ходом. Ситуация, когда в куче 19 или 20 камней, уже разобрана в п. 2. В этих ситуациях игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.
В таблице изображено дерево возможных партий при описанной стратегии Ванн. Заключительные позиции (в них выигрывает Ваня) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в пять раз. Игра завершается в тот момент, когда количество камней в куче становится не менее 69. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 69 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 68.
Задание 1. а) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S. б)Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.
Задание 2. Укажите 2 таких значения S, при которых у Паши есть выигрышная стратегия, причём Паша не может выиграть за один ход и может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.
Задание 3. Укажите хотя бы одно значение S, при котором у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы).
Пояснение
Задание 1.
а) ≥14. При количестве камней в куче от 14 и больше Паше необходимо увеличить количество камней в пять раз, тем самым получив 70 или более камней.
б) 13. Паша своим первым ходом может сделать 14, 17 или 65 камней, после этого Вася увеличивает количество камней в пять раз, получая 70, 85 или 325 камней в куче.
Задание 2.
9, 12. Для данных случаев Паше необходимо прибавить 4 камня к куче из 9 камней, либо 1 камень к куче из 12 камней, и получить кучу из 13 камней. После чего игра сводится к стратегии, описанной в пункте 1б.

Задание 3.
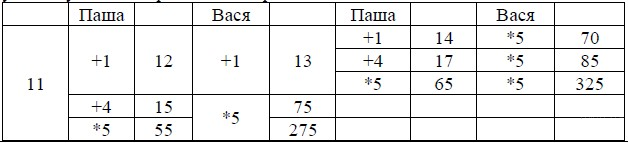
8. Своим первым ходом Паша может сделать количество камней в куче 9, 12 или 40. Если Паша делает ход «увеличить в пять раз», тогда Вася выигрывает своим первым ходом, увеличивая количество камней в пять раз.
Для случая 9 и 12 камней Вася использует стратегию, указанную в п.2.
Данную стратегию можно представить в виде таблицы.
ИЛИ
11. Своим первым ходом Паша может сделать 12, 15 или 55 камней. Если количество камней в куче 15 или 55 Васе необходимо увеличить количество камней в 5 раз. Для случая 12 камней Вася использует стратегию, указанную в п.2. Представим стратегию в виде табли
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 94. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 94 или больше камней.
В начальный момент в куче было S камней; 1 ≤ S ≤ 93.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
Задание 1
а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающие ходы.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 2
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
– Петя не может выиграть за один ход;
– Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для каждого указанного значения S опишите выигрышную стратегию Пети.
Задание 3
Укажите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рисунке на рёбрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции.
Пояснение
1. а) Петя может выиграть, удвоив количество камней в куче, если S = 47, … 93. При меньших значениях S за один ход нельзя получить кучу, в которой не менее 94 камней.
1. б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 46 камней. Тогда после первого хода Пети в куче будет 47 камней или 92 камня. В обоих случаях Ваня удваивает количество камней и выигрывает в один ход.
2. Возможные значения S: 23, 45. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 46 камней. Эта позиция разобрана в п. 1б. В ней игрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (т.е. Петя) следующим ходом выиграет.
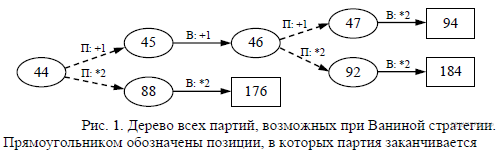
3.Возможное значение S: 44. После первого хода Пети в куче будет 45 или 88 камней. Если в куче станет 88 камней, Ваня удвоит количество камней и выиграет первым ходом. Ситуация, когда в куче 45 камней, разобрана в п. 2. В этой ситуации игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.
В таблице изображено дерево возможных партий при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).
| |
Положения после очередных ходов |
| И.п. |
1-й ход Пети (разобраны все ходы) |
1-й ход Вани (только ход по стратегии) |
2-й ход Пети (разобраны все ходы) |
2-й ход Вани (только ход по стратегии) |
| 44 |
44 + 1 = 45 |
45 + 1 = 46 |
46 + 1 = 47 |
47*2 = 94 |
| 46*2 = 92 |
92*2 = 184 |
| 44*2 = 88 |
88*2 = 176 |
|
|
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 47. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 47 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 46.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Задание 1.
а) При каких значениях числа S Петя может выиграть в один ход?
Укажите все такие значения.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 2.
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход, но (б) Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.
Для указанного значения S опишите выигрышную стратегию Пети.
Задание 3.
Укажите значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, однако у Вани нет стратегии, которая позволит ему гарантированно выиграть 1-м ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в позиции.
Пояснение
а) При каких значениях числа S Петя может выиграть в один ход?
Укажите все такие значения.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 2.
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход, но (б) Петя может выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.
Для указанного значения S опишите выигрышную стратегию Пети.
Задание 3.
Укажите значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, однако у Вани нет стратегии, которая позволит ему гарантированно выиграть 1-м ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах — количество камней в позиции.
Пояснение.
Задание 1.
а) Петя может выиграть, если S = 24, …, 46. При меньших значениях S за один ход нельзя получить кучу, в которой больше 46 камней. б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 23 камня. Тогда после первого хода Пети в куче будет 24 камня, или 25 камней, или 46 камней. Во всех случаях Ваня удваивает количество камней и выигрывает первым ходом.
Задание 2.
Возможные значения S: 21, 22. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 23 камней. Эта позиция разобрана в п. 1б. В ней игрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (то есть Петя) следующим ходом выиграет.
Задание 3.
Возможное значение S: 20. После первого хода Пети в куче будет 21, 22 или 40 камней. Если в куче станет 40 камней, Ваня удвоит количество камней и выиграет первым ходом. Ситуации, когда в куче 21 или 22 камня, уже разобраны в п. 2. В этих ситуациях игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.
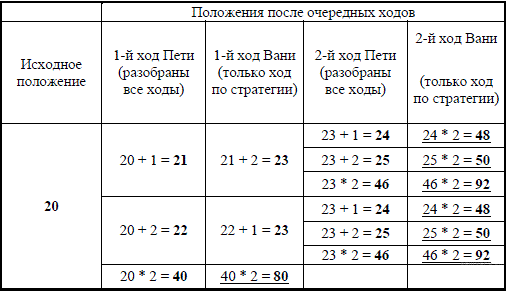
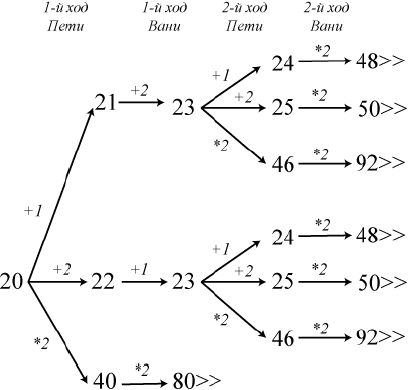
В таблице изображено дерево возможных партий при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчеркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 2, а во второй — 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди, первый ход делает Петя. Ход состоит в том, что игрок или утраивает число камней в какой-то куче, или добавляет 4 камня в какую-то кучу. Игра завершается в тот момент, когда общее число камней в двух кучах становится не менее 32. Если в момент завершения игры количество камней в одной из куч не менее 36, то выиграл Ваня, в противном случае — Петя. Кто выигрывает при безошибочной игре обоих игроков? Каким должен быть первый ход выигрывающего игрока?
Ответ обоснуйте.
Пояснение
Выигрывает Ваня.
Для доказательства рассмотрим неполное дерево игры, оформленное в виде таблицы, где в каждой ячейке записаны пары чисел, разделённые запятой. Эти числа соответствуют количеству камней на каждом этапе игры в первой и второй кучах соответственно.
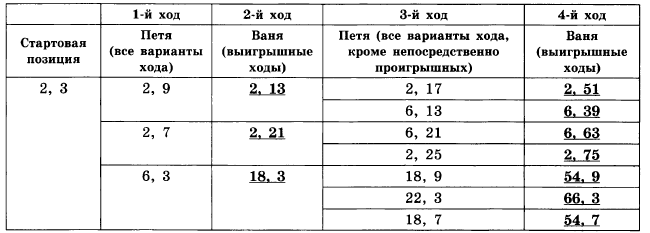
Таблица содержит все возможные варианты ходов первого игрока. Из неё видно, что при любом ходе первого игрока у второго имеется ход, приводящий к победе.
Ваш ответ:
Вы пропустили вопрос
Вопрос 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 25. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 25 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 24.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
1. а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
2. Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход и (б) Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети.
3. Укажите значение S, при котором:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах — количество камней в куче.
Пояснение
1а) Петя может выиграть, если S = 13, …, 24. Во всех этих случаях достаточно удвоить количество камней. При меньших значениях S за один ход нельзя получить кучу, в которой больше 24 камней.
1б) Ваня может выиграть первым ходом (как бы ни играл Петя), если исходно в куче будет S = 12 камней. Тогда после первого хода Пети в куче будет 13 камней или 24 камня. В обоих случаях Ваня удваивает количество камней и выигрывает в один ход.
2. Возможные значения S: 6 и 11. В этих случаях Петя, очевидно, не может выиграть первым ходом. Однако он может получить кучу из 12 камней: в первом случае удвоением, во втором добавлением одного камня. Эта позиция разобрана в п. 1б. В ней игрок, который будет ходить (теперь это Ваня), выиграть не может, а его противник (то есть Петя) следующим ходом выиграет.
3. Возможное значение S: 10. После первого хода Пети в куче будет 11 или 20 камней, Если в куче станет 20 камней, Ваня удвоит количество камней и выиграет первым ходом. Ситуация, когда в куче 11 камней, разобрана в п. 2. В этой ситуации игрок, который будет ходить (теперь это Ваня), выигрывает своим вторым ходом.
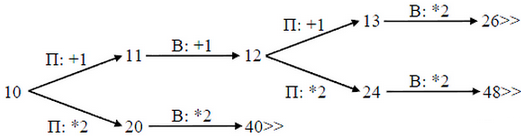
В таблице изображено дерево возможных партий при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчёркнуты. На рисунке это же дерево изображено в графическом виде (оба способа изображения дерева допустимы).
| |
Положения после очередных ходов |
| И.п. |
1-й ход Пети (разобраны все ходы) |
1-й ход Вани (только ход по стратегии) |
2-й ход Пети (разобраны все ходы) |
2-й ход Вани (только ход по стратегии) |
| 10 |
10 + 1 = 11 |
11 + 1 = 12 |
12 + 1 = 13 |
13*2 = 26 |
| 12*2 = 24 |
24*2 = 48 |
| 10*2 = 20 |
20*2 = 40 |
|
Ваш ответ:
Вы пропустили вопрос















