Заметим, что первое и второе уравнения не связаны между собой ни через какие переменные.
Рассмотрим первое уравнение. Для того, чтобы равенство выполнялось, необходимо, чтобы каждая скобка была истинной. Импликация ложна только тогда, когда посылка истинна, а следствие ложно. Представим решение этого уравнения в виде дерева.
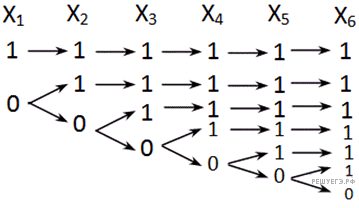
Рассмотрим второе уравнение. Чтобы равенство выполнялось, необходимо, чтобы каждая скобка была истинной. Дерево для решения этого уравнения будет выглядеть так:
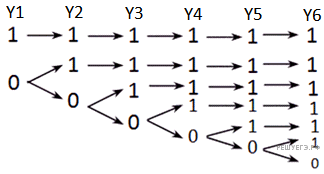
Теперь рассмотрим третье уравнение. Конъюнкция истинна только, если все операнды истинны. Каждое уравнения вида ¬xN ∨ yN = 1 имеет три решения: 01, 00, 11. То есть для каждой пары xN, yN запрещены решения вида 10.
Будем представлять решения уравнений в виде набора нулей и единиц, например, решение x1 = 0, x2 = x3 =x4, = x5= x6 = 1 имеет вид 011 111. Заметим, что для первых двух уравнений в наборах решений после единицы могут стоять только единицы. То есть разрешены решения вида 001 111.
Также заметим, что если yN = 0, то xN обязательно равно единице.
Таким образом, получаем, что набору yN 111 111, могут соответствовать наборы xN: 111 111, 011 111, 001 111, 000 111, 000 011, 000 001, 000 000. Всего семь наборов.
Аналогично, набору yN 011 111 соответствует шесть наборов и так далее. Всего получаем:
7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 наборов.

