Русский язык (Определение главной информации текста)
Результаты теста
Затрачено времени:
00:54:36
Вопрос 15
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?
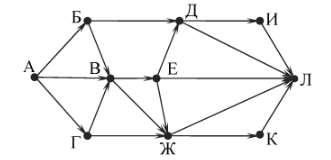
Пояснение
Начнем считать количество путей с конца маршрута – с города Л. NX — количество различных путей из города А в город X, N — общее число путей.
В "Л" можно приехать из И, Д, Е, Ж или К, поэтому N = NЛ = NИ + N Д + N Е + N Ж + N К (*)
Аналогично:
NИ = NД = 4;
NД = NБ + NЕ = 1 + 3 = 4;
NЕ = NВ = 3;
NЖ = NЕ + NВ + NГ = 3 + 3 + 1 = 7;
NК = NЖ = 7.
Добавим еще вершины:
NБ = N А = 1;
NВ = NА + NБ + NГ = 1 + 1 + 1 = 3;
NГ = NА = 1.
Подставим в формулу (*):
N = NЛ = 4 + 4 + 3 + 7 + 7 = 25.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Н, проходящих через город Д?
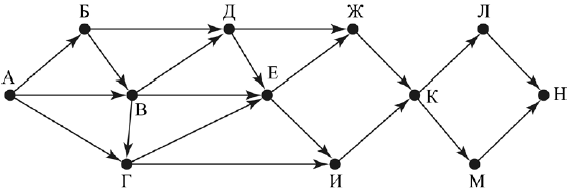
Пояснение
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
При этом, если путь не должен проходить через какой-то город, нужно просто не учитывать этот город при подсчёте сумм. А если город, наоборот, обязательно должен лежать на пути, тогда для городов, в которые из нужного города идут дороги, в суммах нужно брать только этот город.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
А = 1.
Б = А = 1.
В = А + Б = 2.
Г = А + В = 3.
Д = В + Б = 3.
Е = Д = 3 (В и Г не учитываем, поскольку путь должен проходить через город Д).
Ж = Д + Е = 6.
И = Е = 3.
К = Ж + И = 9.
Л = К = М = 9.
Н = Л + М = 18.
Примечание. Необходимо найти количество различных путей из города А в город Н, проходящих через город Д.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город И?
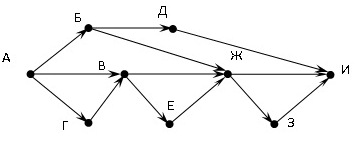
Пояснение
Начнем считать количество путей с конца маршрута – с города И. NX — количество различных путей из города А в город X, N — общее число путей.
В "И" можно приехать из Д, Ж, или З, поэтому N = NИ = NД + NЖ + N З (1)
Аналогично:
NД = NБ;
NЖ = NБ + NВ + NЕ;
NЗ = NЖ.
Добавим еще вершины:
NБ = NА = 1;
NВ = NА + NГ = 1 + 1 = 2;
NЕ = NВ = 2;
NГ = NА = 1;
Преобразуем первые вершины с учетом значений вторых:
NД = NБ = 1;
NЖ = NБ + NВ + NЕ = 1 + 2 + 2 = 5;
NЗ = NЖ = 5.
Подставим в формулу (1):
N = NК = 1 + 5 + 5 = 11.
Начнем считать количество путей с конца маршрута – с города И. NX — количество различных путей из города А в город X, N — общее число путей.
В "И" можно приехать из Д, Ж, или З, поэтому N = NИ = NД + NЖ + N З (1)
Аналогично:
NД = NБ;
NЖ = NБ + NВ + NЕ;
NЗ = NЖ.
Добавим еще вершины:
NБ = NА = 1;
NВ = NА + NГ = 1 + 1 = 2;
NЕ = NВ = 2;
NГ = NА = 1;
Преобразуем первые вершины с учетом значений вторых:
NД = NБ = 1;
NЖ = NБ + NВ + NЕ = 1 + 2 + 2 = 5;
NЗ = NЖ = 5.
Подставим в формулу (1):
N = NК = 1 + 5 + 5 = 11.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город M?
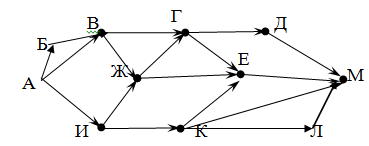
Пояснение
Начнем считать количество путей с конца маршрута – с города М. NX — количество различных путей из города А в город X, N — общее число путей.
В "М" можно приехать из Д, Е, К или Л, поэтому N = NМ = NД + NЕ + N К + N Л (1)
Аналогично:
NД = NГ;
NЕ = NГ + NЖ + NК;
NК = NИ,
NЛ = NК.
Добавим еще вершины:
NГ = NВ + NЖ;
NЖ = NВ + NИ;
NИ = NА = 1;
NВ = NБ + NА = 2;
NБ = NА = 1.
Преобразуем вершины:
NГ = NВ + NЖ = 2 + 3 = 5;
NЖ = NВ + NИ = 2 + 1 = 3;
NИ = NА = 1;
NВ = NБ = 1;
NБ = NА = 1.
NД = NГ = 5;
NЕ = NГ + NЖ + NК = 5 + 3 + 1 = 9;
NК = NИ = 1,
NЛ = NК = 1.
Подставим в формулу (1):
N = NМ = 5 + 9 + 1 + 1 = 16.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке – схема дорог, связывающих города A, B, C, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город E?
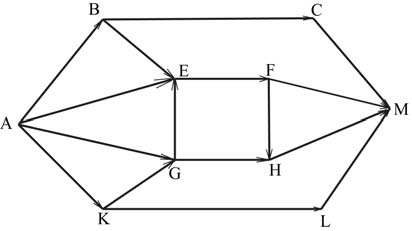
Пояснение
Начнем считать количество путей с конца маршрута – с города E. NX — количество различных путей из города А в город X, N — общее число путей.
В "Е" можно приехать из В, Е, или G, поэтому N = NE = NB + NA + N G(1)
Аналогично:
NB = NA = 1;
NA = 1;
NG = NA + NK = 2;
Подставим в формулу (1):
N = NК = 1 + 1 + 2 = 4.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л?
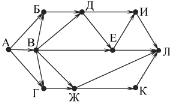
Пояснение
Начнем считать количество путей с конца маршрута – с города Л. NX — количество различных путей из города А в город X, N — общее число путей.
В "Л" можно приехать из И, Е, Ж или К, поэтому N = NЛ = NИ + N Е + N Ж + N К (*)
Аналогично:
NИ = NД + NЕ = 3 + 4 = 7;
NЕ = NД + NВ = 3 + 1 = 4;
NЖ = NВ + N Г = 1 + 2 = 3;
NК = NЖ = 3.
Добавим еще вершины:
NД = NБ + N В = 2 + 1 = 3;
NВ = NА = 1;
NГ = NА + N В = 1 + 1 = 2;
NБ = N А + N В = 1 + 1 = 2.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р, Т. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Т?
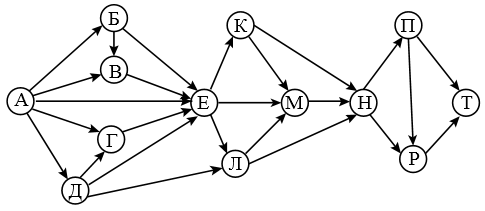
Пояснение
Количество путей до города Х = количество путей добраться в любой из тех городов, из которых есть дорога в Х.
С помощью этого наблюдения посчитаем последовательно количество путей до каждого из городов:
А = 1
Б = А = 1
Д = А = 1
Г = А + Д = 1 + 1 = 2
В = А + Б = 1 + 1 = 2
Е = А + Б + В + Г + Д= 1 + 1 + 2 + 2 + 1 = 7
К = Е = 7
Л = Е + Д = 7 + 1 = 8
М = Е + Л + К = 7 + 8 + 7 = 22
Н = М + К + Л = 22 + 7 + 8 = 37
П = Н = 37
Р = Н + П = 37 + 37 =74
Т = Р + П = 74 + 37 = 111
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F, G, H, K, L, M. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города A в город M?
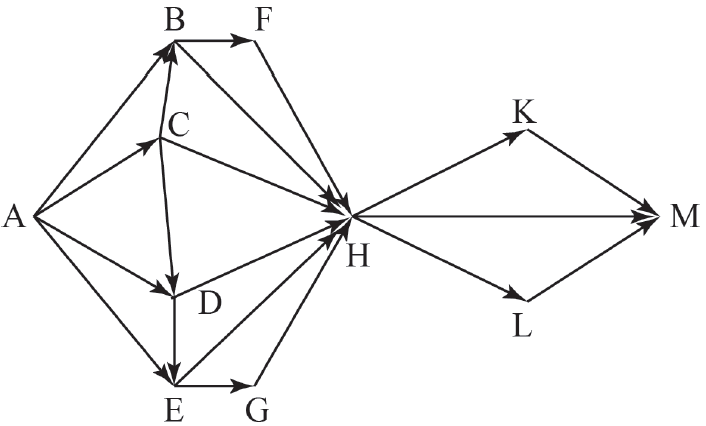
Пояснение
Начнем считать количество путей с конца маршрута – с города М. NX — количество различных путей из города А в город X, N — общее число путей.
В "М" можно приехать из K, H или L, поэтому N = NM = NK + NH + N L (1)
Аналогично:
NK = NH;
NH = NF + NB + NC + ND + NG + NE;
NL = NH.
Добавим еще вершины:
NF = NB = 2;
NB = NA + NC = 2;
NC = NA = 1;
ND = NA + NC = 2;
NE = ND + NA = 2 + 1 = 3;
NG = NE = 3.
Тогда:
NH = 2 + 2 + 1 + 2 + 3 + 3 = 13;
NK = 13;
NL = 13.
Подставим в формулу (1): N = 3 · NH = 3 · 13 = 39.
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р, Т. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Т?
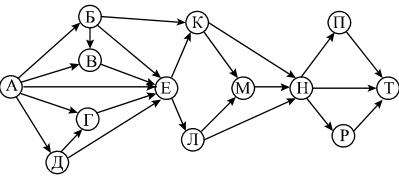
Пояснение
Количество путей до города Х = количеству путей добраться в любой из тех городов, из которых есть дорога в Х.
С помощью этого наблюдения подсчитаем последовательно количество путей до каждого из городов:
А = 1
Б = А = 1
Д = А = 1
Г = А + Д = 1 + 1 = 2
В = А + Б = 1 + 1 = 2
Е = А + Б + В + Г + Д= 1 + 1 + 2 + 2 + 1 = 7
К = Е + Б = 7 + 1 =8
Л = Е = 7
М = Л + К = 8 + 7 = 15
Н = М + К + Л = 15 + 7 + 8 = 30
П = Н = Р = 30
Т = Р + П + Н = 30+ 30 + 30 = 90
Ваш ответ:
Вы пропустили вопрос
Вопрос 15
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
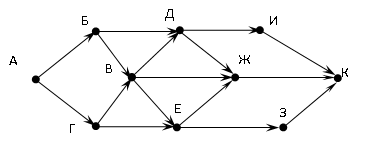
Пояснение
Начнем считать количество путей с конца маршрута – с города К. NX — количество различных путей из города А в город X, N — общее число путей.
В "К" можно приехать из И, Ж, или З, поэтому N = NК = NИ + NЖ + N З (1)
Аналогично:
NИ = NД;
NЖ = NД + NВ + NЕ;
NЗ = NЕ.
Добавим еще вершины:
NД = NБ + NВ ;
NВ = NБ + NГ;
NЕ = NВ + NГ ;
NГ = NА = 1;
NБ = NА = 1.
Преобразуем вершины:
NД = NБ + NВ = 1 + 2 = 3;
NВ = NБ + NГ = 1 + 1 = 2;
NЕ = NВ + NГ = 2 + 1 = 3;
NГ = NА = 1;
NБ = NА = 1.
NИ = NД = 3;
NЖ = NД + NВ + NЕ = 3 + 2 + 3 = 8;
NЗ = NЕ = 3.
Подставим в формулу (1):
N = NК = 3 + 8 + 3 = 14.
Ваш ответ:
Вы пропустили вопрос











